一、信道编码基础概述
1. 信道编码目的
信道编码(Channel Coding)是一种在数据传输前对信息进行冗余编码的技术,用于提高通信系统在信道干扰、噪声等条件下的抗误码能力。
其核心思想是:
在原始信息中添加冗余信息,使得接收端可以检测甚至纠正在传输过程中产生的错误。
2. 编码率定义
信道编码引入了“冗余比特”,其编码效率通常由编码率(Code Rate)R来衡量:
\[R=\frac{K}{N}\]𝐾 信息比特数(原始数据)
𝑁 编码后比特数(含冗余)
𝑅∈(0,1]:值越大,说明冗余越少,效率越高
3. 本文介绍的编码
| 编码类型 | 特点说明 |
|---|---|
| 重复码 | 简单,每比特重复多次 |
| 奇偶校验码 | 仅能检测偶数/奇数错误 |
| 汉明码 | 可纠1位、检2位错 |
| 卷积码 | 实时编码,结构灵活 |
二、重复码
1. 基本原理
重复码是一种最简单的信道编码方式,其思想是:
将每个信息比特重复多次发送,从而增加抗干扰能力。
例如,若原始比特为:
1 0 1
设定重复次数 n=3,编码后为:
1 1 1 0 0 0 1 1 1
重复码能有效对抗噪声,但效率较低,属于典型的冗余换可靠性策略。
2. MATLAB 示例:重复编码流程
% 1. 原始比特
num_bits = 3;
msg = randi([0 1], 1, num_bits);
fprintf('原始数据: %s\n', num2str(msg));
% 2. 重复编码(每比特重复n次)
n = 3;
coded_bits = repelem(msg, n);
fprintf('重复编码后数据: %s\n', num2str(coded_bits));
示例输出:
原始数据: 1 0 1
重复编码后数据: 1 1 1 0 0 0 1 1 1
3. 重复码的BER性能仿真
在 BPSK + AWGN 信道下,使用多数表决方式解码。即将接收到的多个重复位进行加权求和,若和为正,则判为1,否则判为0。
% 参数设置
n = 2; % 重复次数
num_bits = 10000;
EbN0_dB = -10:1:10;
ber = zeros(size(EbN0_dB));
for idx = 1:length(EbN0_dB)
% 1. 原始比特
msg = randi([0 1], 1, num_bits);
% 2. 重复编码
coded_bits = repelem(msg, n);
% 3. BPSK调制
tx_symbols = 2 * coded_bits - 1;
% 4. AWGN信道
EbN0 = 10^(EbN0_dB(idx)/10);
noise_var = 1/(EbN0);
% 这里是实信号,所以这边不需要除以2;如果是复信号,需要除以2
noise = sqrt(noise_var) * randn(size(tx_symbols));
rx_symbols = tx_symbols + noise;
% 5. 多数表决解码
rx_matrix = reshape(rx_symbols, n, []);
symbol_sum = sum(rx_matrix);
decoded_bits = symbol_sum > 0;
% 6. 计算BER
[~, ber(idx)] = biterr(msg, decoded_bits);
end
% 7. 绘图
figure;
semilogy(EbN0_dB, ber, '-o', 'LineWidth', 2);
grid on;
xlabel('E_b/N_0 (dB)');
ylabel('Bit Error Rate (BER)');
title(sprintf('重复码 (n = %d) 在AWGN信道下的BER性能', n));
以下给出仿真曲线:
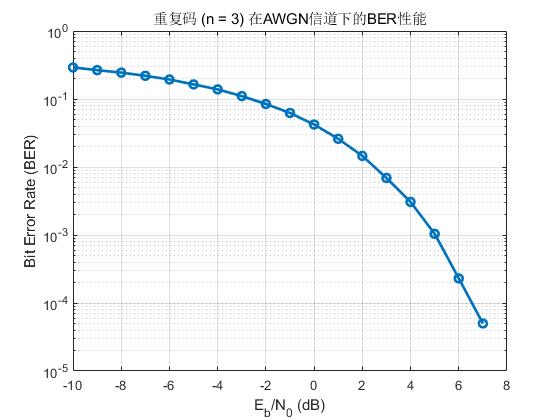
下图给出重复码在不同重复次数下曲线:
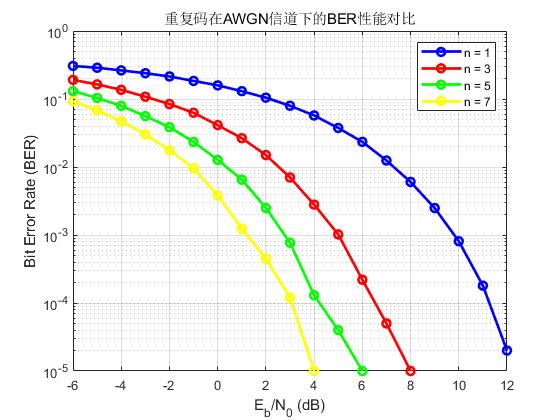
三、奇偶校验码(Parity Check Code)
1. 基本原理
奇偶校验码是一种简单的错误检测码,通过在数据后添加一个校验位(parity bit)来判断数据在传输中是否出错。
奇校验(odd parity): 校验后整个码字的“1”的个数为奇数;
偶校验(even parity): 校验后整个码字的“1”的个数为偶数;
该方法只能检测奇数个错误,不能纠正错误,也无法检测偶数位同时出错的情况。
2. MATLAB 示例:奇校验编码与检测
clc; clear;
% 原始数据(8位)
data = [1 0 0 1 0 1 1 0 0];
% 1. 编码:添加奇校验位
if mod(sum(data), 2) == 0
parity_bit = 1; % 原本是偶数,补1变成奇数
else
parity_bit = 0; % 原本是奇数,补0保持奇数
end
tx = [data parity_bit]; % 添加校验位,构成传输比特流
fprintf('原始数据: %s\n', num2str(data));
fprintf('添加奇校验位后: %s\n', num2str(tx));
%% 2. 模拟传输过程中的错误(控制错误位置)
% 情况A:传输中没有错误
rx1 = tx;
% 情况B:单比特错误(改变第5位)
rx2 = tx; rx2(3) = mod(rx2(3)+1, 2);
% 情况C:双比特错误(改变第1和3位)
rx3 = tx; rx3([1 3]) = mod(rx3([1 3])+1, 2);
%% 3. 检测函数
detect_parity_error = @(vec) mod(sum(vec), 2) == 1;
%% 4. 判定并输出
fprintf('\n情况A:无错误 %s → %s\n', num2str(rx1), ...
ternary(detect_parity_error(rx1), '无错', '检测到错误'));
fprintf('情况B:1位错误 %s → %s\n', num2str(rx2), ...
ternary(detect_parity_error(rx2), '无错', '检测到错误'));
fprintf('情况C:2位错误 %s → %s\n', num2str(rx3), ...
ternary(detect_parity_error(rx3), '无错', '检测到错误'));
function result = ternary(condition, valTrue, valFalse)
if condition
result = valTrue;
else
result = valFalse;
end
end
3. 如何理解奇偶校验判断
detect_parity_error = @(vec) mod(sum(vec), 2) == 1;
这是一句 匿名函数定义,定义了一个函数 detect_parity_error,它的作用是:
判断一个比特序列的奇偶校验是否通过(按奇校验规则)
其中:
| 组成部分 | 说明 |
|---|---|
@ | 表示匿名函数的起始(没有函数名) |
(vec) | 函数的输入参数,vec 是一个比特向量 |
sum(vec) | 计算该比特向量中所有元素之和(即 1 的个数) |
mod(..., 2) | 求该和对 2 的模,即判断总和是奇数(1)还是偶数(0) |
== 1 | 判断结果是否为奇数(1) |
| 最终结果 | 如果是奇数,则返回 true,表示“奇数个1”——奇校验 通过(无错)如果是偶数,则返回 false,表示“偶校验失败”——检测到错误 |
四、汉明码(Hamming Code)
1. 基本原理
汉明码(Hamming Code)是一种经典的纠错码,可以检测并纠正 1 位错误,其本质是奇偶校验的“升级版”。
它通过在原始数据中插入多个“奇偶校验位”,使得在接收端能根据特定的校验规则定位出出错位。
2. 冗余位(Parity Bit)数量计算
对于 𝑚 个数据位,需要添加 𝑟 个冗余位,使得:
\[2^r \geq m+r+1\]𝑚:原始数据位数
𝑟:冗余位个数
📌 例如:
若 𝑚=7,则最小满足不等式的 𝑟=4,因为:
\[2^4=16 \geq 7+4+1=12\]此时,整个码字长度为 7+4=11 位
3. 编码结构(以11位汉明码为例)
通常采用“位置法”插入冗余位,即:
在 1、2、4、8 等2的幂次位插入校验位
剩余位置填入数据位
例如(从左到右标号1~11):
| 位置编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 内容 | P1 | P2 | D1 | P3 | D2 | D3 | D4 | P4 | D5 | D6 | D7 |
其中:
Pi 表示第 i 个奇偶校验位
Di 表示第 i 个数据位
4. MATLAB 示例:汉明码(7,4)仿真
下面是一个使用 MATLAB 进行 7→11 汉明码编码 + 加错 + 解码纠错的完整流程。
clc; clear;
% 原始数据:7位
% data = [1 0 1 1 0 0 1]; % 示例数据,可改为 randi([0 1],1,7)
data = [1 0 0 1 1 0 1];
fprintf('编码前数据: %s\n', num2str(data));
% 初始化11位码字(含4个校验位)
code = zeros(1,11);
% 插入数据位
data_idx = setdiff(1:11, [1 2 4 8]); % 非2的幂次是数据位
code(data_idx) = data;
% 计算校验位:使用奇校验规则
parity_pos = [1 2 4 8];
for i = 1:length(parity_pos)
pos = parity_pos(i);
covered = find(bitand(1:11, pos)); % 找出被当前校验位覆盖的位置
code(pos) = mod(sum(code(covered))+1, 2); % 奇偶校验
end
fprintf('编码后的汉明码:%s\n', num2str(code));
%% 模拟信道错误(第5位翻转)
err_code = code;
err_code(5) = mod(err_code(5)+1, 2); % 加入1位错误
%% 解码:计算 syndrome(综合错误位)
syndrome = 0;
for i = 1:length(parity_pos)
pos = parity_pos(i);
covered = find(bitand(1:11, pos));
parity = mod(sum(err_code(covered))+1, 2);
syndrome = syndrome + parity * pos;
end
fprintf('接收码字: %s\n', num2str(err_code));
fprintf('syndrome(二进制位置):%d\n', syndrome);
%% 如果 syndrome ≠ 0,说明有错误,定位并纠正
if syndrome ~= 0
fprintf('检测到错误,位置:%d,已纠正。\n', syndrome);
err_code(syndrome) = mod(err_code(syndrome)+1, 2);
else
fprintf('未检测到错误。\n');
end
%% 提取数据位
decoded_data = err_code(data_idx);
fprintf('解码后数据: %s\n', num2str(decoded_data));
5. 特点总结
| 特性 | 说明 |
|---|---|
| 检测能力 | 可检测 1 位、2 位错误 |
| 纠错能力 | 可纠正 1 位错误 |
| 码率 | 例如 7 位数据 + 4 校验 → 码率为 7/11 ≈ 0.636 |
| 典型应用 | 内存(ECC)、卫星通信、基础数据传输 |
五、卷积码
1. 基本原理
卷积码是一种将原始比特序列连续编码的纠错编码方式,每个输出码字不仅依赖当前输入比特,还与前面若干个输入有关,具有“记忆”特性。
其本质是:
将输入序列卷积到多个输出中,增强了错误检测与纠正能力。
2. 卷积编码结构
卷积码通常使用三元组表示为:
\[(n, K, N)\]| 参数 | 含义 |
|---|---|
| \(K\) | 每次输入的比特数(原始比特数) |
| \(n\) | 每次输出的比特数(编码后比特数) |
| \(N\) | 编码器的约束长度,等于寄存器个数+1,表示输出受影响的输入比特段数 |
编码率为:
\[R = \frac{K}{n}\]3. 编码原理简述
卷积码通过一组移位寄存器和模2加法器(XOR门)实现。当每个输入比特流入时,会影响接下来多个时刻的输出:
前输出 = 当前输入比特 + 前 𝑁−1 位输入比特的线性组合
4. 示例:(3,1,3) 卷积码
每次输入 1 个比特(𝐾=1)
每次输出 3 个比特(𝑛=1)
约束长度为3,表示输出与当前和前2个输入有关(𝑁=3)
编码率 1/3
(a) 框图表示
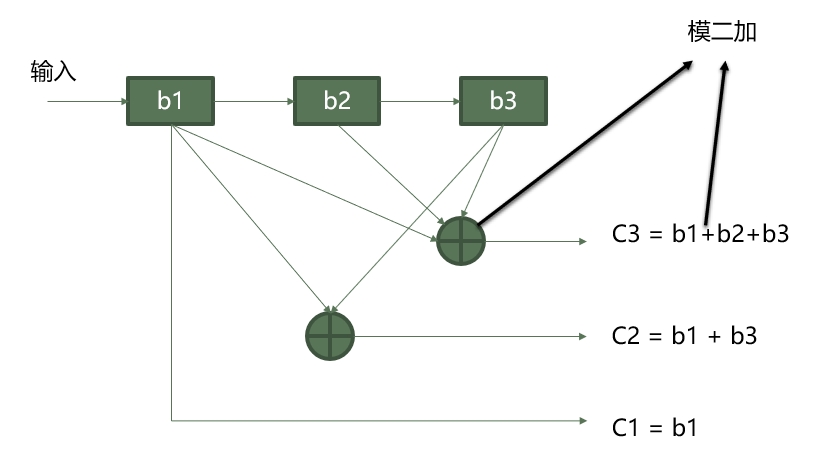
根据图中标注,有如下关系:
\[C_1 = b_1\] \[C_2 = b_1 + b_3\] \[C_3 = b_1+b_2+b_3\]说明:所有加法均为模2加,即 XOR 操作。
(b) 生成多项式表示(八进制)
将每个输出支路的加法结构转化为生成多项式,对应:
| 支路 | 多项式(2进制) | 八进制表示 |
|---|---|---|
| \(C_1\) | 001 | 1 |
| \(C_2\) | 101 | 5 |
| \(C_3\) | 111 | 7 |
所以该卷积码可表示为:
\[G=\left[\begin{array}{lll} 1 & 5 & 7 \end{array}\right]_8\](c) MATLAB实现
下面给出 MATLAB 对于上述 (3,1,3) 编码器的手动实现
假设输入比特序列为1011。(此处不考虑尾比特冲刷)
clc; clear;
% 输入比特序列
u = [1 0 1 1]; % 输入长度为4
L = length(u); % 原始长度
m = 2; % 寄存器数量(约束长度N=3)
% 状态初始化
reg = zeros(1, m); % 两个寄存器(b2、b3)
encoded = []; % 输出码字序列
% 卷积码生成规则
% C1 = b1
% C2 = b1 + b3
% C3 = b1 + b2 + b3
for i = 1:L
b1 = u(i);
b2 = reg(1);
b3 = reg(2);
% 三个支路计算(模2加)
c1 = mod(b1, 2);
c2 = mod(b1 + b3, 2);
c3 = mod(b1 + b2 + b3, 2);
encoded = [encoded, c1, c2, c3];
% 更新寄存器状态
reg = [b1, reg(1)];
end
% 输出结果
disp('输入比特序列:');
disp(u);
disp('卷积编码输出序列(并联):');
encoded_p = reshape(encoded, 3, []);
disp(encoded_p.');
disp('卷积编码输出序列(串联):');
disp(encoded);
如何通过 MATLAB自带的卷积编码函数实现。上述实现的是一个系统卷积码(systematic convolutional code):
即:编码输出中包含原始比特作为一部分输出,另外的输出则是冗余比特。
❗ 而 MATLAB 默认的 convenc() 是非系统卷积码(Non-Systematic):
输出的所有比特都是编码后的结果,原始数据不直接保留;
例如对于
poly2trellis(3, [5 7]),是每个输入对应两个输出。
通过拼接原始数据和校验数据可以得到卷积码系统码
% matlab函数实现
trellis = poly2trellis(3, [5 7]); % 约束长度3,生成多项式[5 7]
data = [1 0 1 1]; % 原始比特流
coded = convenc(data, trellis); % 卷积编码
coded_r = reshape(coded,2,[]);
encoded = [data; coded_r].';
disp('卷积编码输出序列:');
disp(encoded);
5. 维特比译码
维特比译码(Viterbi Decoding)是一种判决译码算法,广泛用于卷积码的译码过程。它的核心思想是通过动态规划,在所有可能的状态转移路径中寻找累积路径度量最小的路径,即最可能的原始比特序列。
(a) 基本原理
- 将卷积码的编码过程建模为一个有向图(Trellis)
- 每一层表示一个时间步,每个节点代表一个可能的状态
- 每条边代表从当前状态接收一个比特后转移到下一状态,并输出对应编码比特
- 对每个时间步,仅保留每个状态中路径度量最小的路径(幸存路径),其余丢弃
- 最终从路径度量最小的终止状态开始回溯,恢复原始输入比特序列
✅ 路径度量:
- 硬判决:使用汉明距离作为度量
- 软判决:使用欧几里得距离或对数似然比(LLR)等度量方式,性能更优
(b) MATLAB 验证
以下模拟一个 (3,1,3) 卷积码系统,对输入比特进行编码、加错误,然后用 Viterbi 算法译码,并将状态转移过程在图中可视化,包括路径选择与输入比特标注。
clc; clear;
u = [1 1 0 1]; % 原始输入
enc = conv_encode_313(u);
% 模拟信道错误(第2和4组)
enc_err = enc;
enc_err(4) = mod(enc_err(4)+1, 2);
enc_err(11) = mod(enc_err(11)+1, 2);
% 解码
[dec,state_path] = viterbi_decode_313(enc_err);
% 显示结果
disp('原始比特:'); disp(u);
disp('编码比特:'); disp(enc);
disp('错误注入后:'); disp(enc_err);
disp('Viterbi译码输出:'); disp(dec);
% 状态定义
states = ["00", "01", "10", "11"];
L = 4; % 解码长度
rx = reshape(enc_err,3,[]).';
% rx = [1 1 1; 0 0 1; 1 0 0; 0 1 0]; % 接收码,含错误
% 所有状态位置布局
figure; hold on;
offsetY = 1.5;
for t = 0:L
for s = 0:3
y = -s * offsetY;
plot(t, y, 'ko', 'MarkerSize', 8, 'LineWidth', 1.5);
text(t, y + 0.4, states(s+1), 'HorizontalAlignment', 'center');
end
end
% 状态转移和边标注(优化版:路径样式 & 标签不重叠)
for t = 0:L-1
for curr = 0:3
b2 = bitget(curr, 2); b3 = bitget(curr, 1);
label_offsets = [-0.2, 0.2]; % 竖直偏移
for in = 0:1
b1 = in;
c1 = mod(b1, 2);
c2 = mod(b1 + b3, 2);
c3 = mod(b1 + b2 + b3, 2);
out = [c1 c2 c3];
ns = bitshift(b1, 1) + b2;
% 汉明距离
hd = sum(rx(t+1,:) ~= out);
% 坐标计算
x = [t, t+1];
y = [-curr*offsetY, -ns*offsetY];
% 线型设置:输入0为实线,1为虚线
if in == 0
lineStyle = '-'; % 实线
else
lineStyle = '--'; % 虚线
end
% 绘制路径
plot(x, y, 'b', 'LineStyle', lineStyle, 'LineWidth', 1);
% 标签设置(交错避免重叠)
label = sprintf('%d%d%d/%d', out(1), out(2), out(3), hd);
midx = mean(x);
midy = mean(y) + label_offsets(in+1);
text(midx, midy, label, ...
'FontSize', 8, 'Color', 'k', 'HorizontalAlignment', 'center');
end
end
end
% 图形设置
title('Viterbi 状态转移图(含路径码字/汉明距离)');
xlabel('时间步骤');
for t = 1:L
prev = state_path(t);
curr = state_path(t+1);
x = [t-1, t];
y = [-prev*offsetY, -curr*offsetY];
plot(x, y, 'r-', 'LineWidth', 3); % 红色粗线表示幸存路径
txt = sprintf('u=%d', dec(t));
midx = (t-1 + t)/2;
midy = ( -state_path(t)*offsetY + -state_path(t+1)*offsetY ) / 2;
text(midx, midy+0.4, txt, 'Color', 'r', 'FontSize', 15, ...
'HorizontalAlignment', 'center');
end
axis off;
axis equal;
下图给出仿真结果,红色标记了译码的路线。
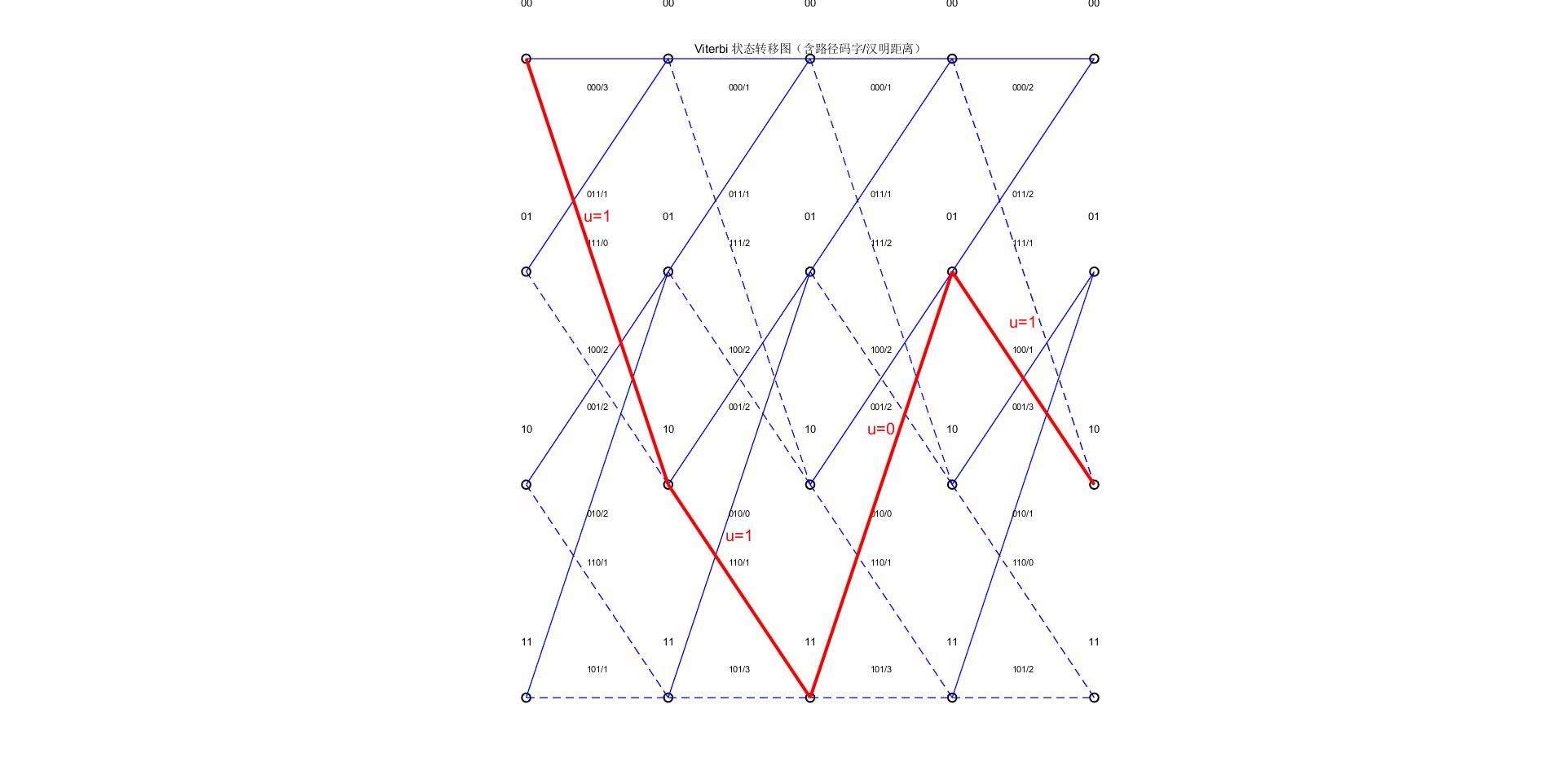
六、总结
信道编码作为通信系统的重要组成,在高可靠性通信需求中发挥关键作用。
本文介绍了重复码、奇偶校验码、汉明码和卷积码等基础信道编码方法,并结合 MATLAB 示例演示了各自的编码与译码过程。
这些基础编码方法虽原理简单,但为理解更复杂的纠错编码(如Turbo码、LDPC码)打下了基础。
文档信息
- 本文作者:Ziyue Qi
- 本文链接:https://www.qiziyue.cn/2025/07/23/%E7%AE%80%E5%8D%95%E7%9A%84%E4%BF%A1%E9%81%93%E7%BC%96%E7%A0%81/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)