一、引言
之前一直有疑问信道的带宽和码率以及香农门限的关系是如何推导的,同时还很疑惑为什么LTE 20M的信道带宽只需要30.72M采样率就够了。
遂重新学习奈奎斯特采样定律相关的知识。
二、奈奎斯特采样定理
1. 原理
要完整、无失真地采样一个信号,采样频率必须至少是信号中最高频率的两倍:
若一个模拟信号带宽为 B Hz(即频谱在 [−B, B] 范围内),则以 fs ≥ 2B 的采样率采样,可以无失真地恢复该信号。
这个最小采样率 fs = 2B 被称为奈奎斯特率(Nyquist rate)。
2. MATLAB验证
下面进行 MATLAB 验证:
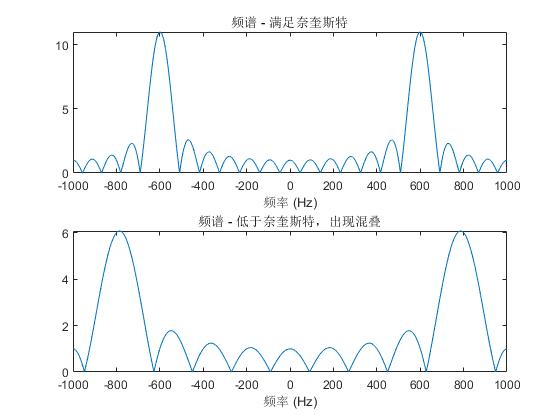
比较“满足奈奎斯特采样率”和“不满足采样率”时,信号频谱的变化,验证混叠现象。
- 模拟信号中含有一个 600Hz 的正弦波分量
- fs1 = 2B → 理论上可完美重建
- fs2 = B → 小于奈奎斯特速率,会出现混叠(aliasing)
% 参数设置
B = 1000; % 模拟信号带宽(Hz)
fs1 = 2*B; % 满足奈奎斯特
fs2 = 1*B; % 低于奈奎斯特
t_max = 0.01; % 信号时间长度
f0 = 600; % 一个在带宽范围内的频率分量
% 采样信号1(fs1 = 2B)
ts1 = 0:1/fs1:t_max;
x1 = cos(2*pi*f0*ts1);
% 采样信号2(fs2 = 1.2B) → 会混叠
ts2 = 0:1/fs2:t_max;
x2 = cos(2*pi*f0*ts2);
% 频谱查看
N = 4096;
f = linspace(-fs1/2, fs1/2, N);
% 可视化
figure;
subplot(2,1,1);
plot(f, abs(fftshift(fft(x1, N))));
title('频谱 - 满足奈奎斯特');
xlabel('频率 (Hz)');
subplot(2,1,2);
plot(f, abs(fftshift(fft(x2, N))));
title('频谱 - 低于奈奎斯特,出现混叠');
xlabel('频率 (Hz)');
运行结果如下:
三、奈奎斯特采样定理的复数扩展
对于实数奈奎斯特定理,由于实值信号的频谱具有共轭对称性,其正负频率内容是冗余的。
然而,在现代通信系统中,信号通常采用复数基带表示。因此,理解奈奎斯特定理在复数信号上的适用条件与扩展形式,对于系统设计、模拟、SDR 等领域至关重要。
1. 实值信号的频谱对称性
设实信号为\(x(t) \in \mathbb{R}\),其傅里叶变换 𝑋(𝑓) 满足满足:
\[X(-f)=X^*(f)\]这意味着:
- 频谱对称 → 正负频率成分相互冗余
- 对一个频率分量 \(f_0\),其共轭对应 \(-f_0\)
易于用MATLAB验证
clear; clc; close all;
% ====== 信号设置 ======
Fs = 1000; % 采样率 Hz
T = 1; % 时间长度 s
t = 0:1/Fs:T-1/Fs; % 时间轴
f0 = 100; % 频率
f1 = 400; % 频率
x = cos(2*pi*f0*t) + 3*sin(2*pi*f1*t); % 实数信号
% ====== 计算 FFT ======
N = length(x);
X = fft(x); % 不做 shift
f = (0:N-1)*(Fs/N); % 单边频率坐标
f_centered = (-N/2:N/2-1)*(Fs/N); % 中心对齐频率轴
% ====== 共轭对称性验证(用前后对称位置比较) ======
% 正频率部分
X_pos = X(2:N/2); % 正频率,去掉DC和Nyquist点
X_neg = X(N:-1:N/2+2); % 负频率,共轭对称点
X_neg_conj = conj(X_neg); % 应该等于 X_pos
% 对应频率轴
f_half = f(2:N/2); % 去掉0Hz和Fs/2
% 幅度图
subplot(2,1,1);
plot(f_half, abs(X_pos), 'b'); hold on;
plot(f_half, abs(X_neg_conj), 'r--');
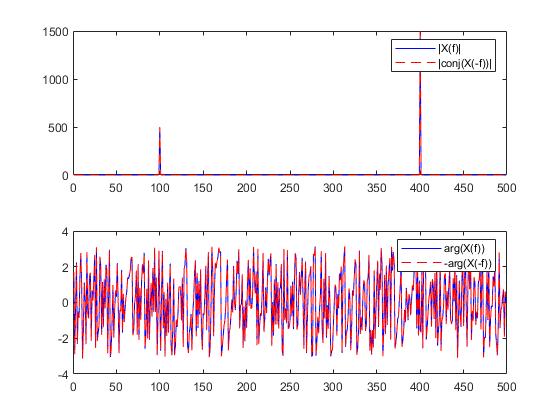
legend('|X(f)|', '|conj(X(-f))|');
% 相位图
subplot(2,1,2);
plot(f_half, angle(X_pos), 'b'); hold on;
plot(f_half, -angle(X_neg), 'r--');
legend('arg(X(f))', '-arg(X(-f))');
可以观察到实信号共轭对称性。
2. 复数信号的频谱结构
与实信号不同,复信号的频谱可以是非对称的,正负频率可携带独立信息。
如:
\[x(t)=e^{j 2 \pi f_0 t} \Rightarrow X(f)=\delta\left(f-f_0\right)\]此信号的频谱仅位于正频率,并不含共轭分量。由此可以引出复数信号下的采样定理。
3. 复数奈奎斯特采样定理
若一个复数信号是严格带限且频谱单边,带宽为 𝐵(频谱范围为 [0,𝐵]),则采样率只需:
\[f_s \geq B\]即可实现无混叠采样。
在实际通信系统中,常见的复数信号(如 OFDM、IQ 信号)通常是双边带宽的,即频谱占据 [−𝐵/2,+𝐵/2],此时带宽仍为 𝐵。
对这种信号,其复数采样仍需满足:
\[f_s \geq B\]4. MATLAB验证
此处构造了复数带通信号(两个不同频率点)
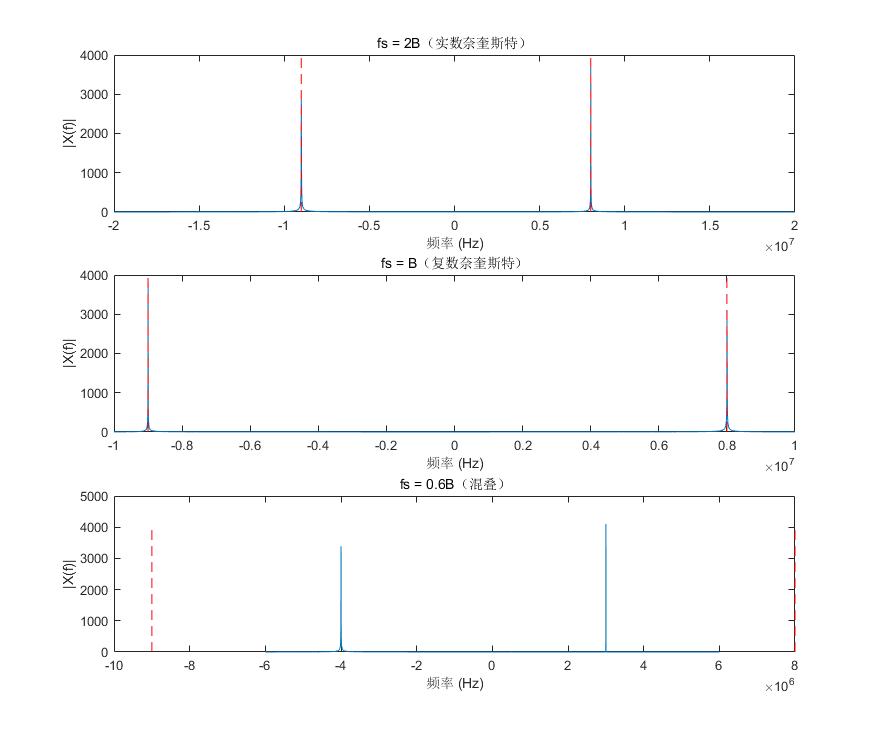
分别用 𝑓𝑠=2𝐵, 𝐵, 0.6𝐵 三种采样率验证。
% 复数信号奈奎斯特采样定理
% 基本参数
B = 20000000; % 信号带宽(Hz)
f0 = -9000000; % 复数信号频率,应满足 f0 < B
f1 = 8000000;
t_max = 0.01;
% 构造连续时间近似
t = linspace(0, t_max, 1e5);
x = exp(1j*2*pi*f0*t)+exp(1j*2*pi*f1*t); % 复数基带信号
% 采样频率设定
fs1 = 2*B; % 实数信号奈奎斯特采样率
fs2 = 1*B; % 复数信号奈奎斯特采样率
fs3 = 0.6*B; % 不满足奈奎斯特(混叠)
% 采样
ts1 = 0:1/fs1:t_max; x1 = exp(1j*2*pi*f0*ts1)+exp(1j*2*pi*f1*ts1);
ts2 = 0:1/fs2:t_max; x2 = exp(1j*2*pi*f0*ts2)+exp(1j*2*pi*f1*ts2);
ts3 = 0:1/fs3:t_max; x3 = exp(1j*2*pi*f0*ts3)+exp(1j*2*pi*f1*ts3);
% FFT 设置
Nfft = 4096;
f_axis1 = linspace(-fs1/2, fs1/2, Nfft);
f_axis2 = linspace(-fs2/2, fs2/2, Nfft);
f_axis3 = linspace(-fs3/2, fs3/2, Nfft);
% 计算频谱
X1 = fftshift(fft(x1, Nfft));
X2 = fftshift(fft(x2, Nfft));
X3 = fftshift(fft(x3, Nfft));
% 绘图
figure;
subplot(3,1,1);
plot(f_axis1, abs(X1)); title('fs = 2B(实数奈奎斯特)');
xlabel('频率 (Hz)'); ylabel('|X(f)|');
hold on; yline = ylim;
plot([f0 f0], yline, 'r--'); plot([f1 f1], yline, 'r--');
subplot(3,1,2);
plot(f_axis2, abs(X2)); title('fs = B(复数奈奎斯特)');
xlabel('频率 (Hz)'); ylabel('|X(f)|');
hold on; yline = ylim;
plot([f0 f0], yline, 'r--'); plot([f1 f1], yline, 'r--');
subplot(3,1,3);
plot(f_axis3, abs(X3)); title('fs = 0.6B(混叠)');
xlabel('频率 (Hz)'); ylabel('|X(f)|');
hold on; yline = ylim;
plot([f0 f0], yline, 'r--'); plot([f1 f1], yline, 'r--');
结果如下:
四、总结
本文阐明了实数与复数信号在采样要求上的本质区别:
实数信号由于其频谱具有共轭对称性,实际有效带宽为双边,因此需满足采样率 𝑓𝑠≥2B 才能完整重建信号,避免频谱混叠。
复数信号若频谱仅分布在单边,正负频率不再冗余,则理论最低采样率仅需满足 𝑓𝑠 ≥ 𝐵,该性质广泛应用于现代通信系统。
进一步地,这些结论也有助于理解 LTE 等通信标准中采样率与信道带宽的匹配关系。
文档信息
- 本文作者:Ziyue Qi
- 本文链接:https://www.qiziyue.cn/2025/07/24/%E5%A5%88%E5%A5%8E%E6%96%AF%E7%89%B9%E9%87%87%E6%A0%B7%E7%9B%B8%E5%85%B3/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)