一、信道编码基础
前文介绍了重复码、奇偶校验码、汉明码和卷积码等基础信道编码方法,并结合 MATLAB 示例演示了各自的编码与译码过程。
本文将介绍 TURBO 和 LDPC 两种在4G和5G中广泛应用的前向纠错码。
以下将先介绍一些基础通信理论。
1. 奈奎斯特采样定理
要完整、无失真地采样一个信号,采样频率必须至少是信号中最高频率的两倍。
在无线通信或有线通信中,奈奎斯特定理也用于决定:
在某个带宽范围内最多能传多少比特/秒?
✅ 奈奎斯特码元速率(Nyquist symbol rate):
在无码间干扰(ISI)的理想情况下,最大码元率 = 2 × 带宽
即:
在带宽为 B Hz 的信道中,每秒最多可以无失真地传 2B 个码元(symbols)。
2. 香农极限公式
香农信道容量公式(Shannon Capacity):
\[C < B \cdot \log _2\left(1+\frac{S}{N}\right)\]其中:
- 𝐶:信道容量(bit/s),即单位时间内可靠传输的最大信息速率
- 𝐵:信道带宽(Hz)
- 𝑆/𝑁:信噪比(功率比)
描述了在给定带宽和信噪比下通信系统的理论极限传输速率。超过该速率将无法实现无错传输。
3. 与码率的关系(Eb/N0 形式)
我们关心的是在单位比特能量(𝐸𝑏)和噪声功率谱密度(𝑁0)下的表现:
目标是从香农公式推出误码性能相关的 Eb/N0 极限表达式。
推导过程如下:
- 定义 \(R\) 为信道比特率(bit/s):
- 代入香农公式
引入 Eb/N0:
- 平均每比特能量为 \(E_b=\frac{S}{R}\)
- 单位噪声功率谱密度 \(N_0=\frac{N}{B}\)
- 因此:
- 代入香农公式并变换:
- 定义带宽归一化速率(即频谱效率)
- 于是得到:
- 整理得到香农极限计算公式:
香农极限表示了在 AWGN 信道中实现可靠通信所需的最小 𝐸𝑏/𝑁0(每比特信噪比)门限.
可以计算得到 1/2 归一化频谱效率下的香农极限为 0 dB。
而当频谱效率趋近于 0(即码率远小于带宽)时,香农极限趋于理论下限 -1.59 dB。
这表明:即便采用无限低速率传输,每个比特的能量也不能低于该极限,这是任何数字通信系统都无法逾越的物理界限。
二、Turbo码
1. 概述
Turbo码由 Claude Berrou 等人于 1993年提出,是一种接近香农极限性能的纠错编码,被称为信道编码领域的里程碑。
- 采用并行级联卷积编码结构;
- 解码采用软输入软输出迭代译码算法;
- 可逼近理论极限误码性能(1/2码率下,其性能距离 Shannon 极限仅约 0.7 dB);
- 解决传统卷积码在低信噪比下性能不佳的问题;
- 引领现代纠错编码体系的发展,促进 3G/4G/5G 等系统演进。
2. 系统码与非系统码
| 项目 | 系统码 | 非系统码 |
|---|---|---|
| 定义 | 原始信息比特 直接出现在输出码字中 | 原始信息不直接出现,仅存在于编码后新的冗余比特中 |
| 结构特征 | 保留原始输入比特,添加校验比特 | 所有输出比特均由编码器结构组合生成 |
| 信息保留性 | ✅ 保留原始数据 | ❌ 不保留 |
(a) 经典非系统码结构(Classical Non-Systematic Code)
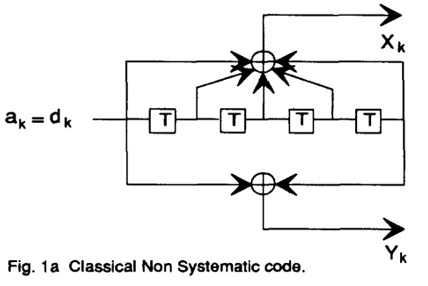
上图给出一个经典非系统码的例子,其特点如下:
- ✅ 前馈结构(Feedforward):编码器结构只依赖当前及过去输入,无内部状态反馈;
- ❌ 无记忆性:编码器输出仅依赖于当前输入,不能形成迭代反馈链路;
其时域表达式为:
\[\begin{gathered} x_k=d_k+d_{k-1}+d_{k-2}+d_{k-3}+d_{k-4} \\ y_k=d_k+d_{k-4} \end{gathered}\]生成多项式:
\[\begin{gathered} g_x(D)=1+D+D^2+D^3+D^4 \\ g_y(D)=1+D^4 \end{gathered}\]输出的多项式乘法表达式也可以写为:
\[\begin{gathered} x(D)=d(D) \cdot g_x(D) \\ y(D)=d(D) \cdot g_y(D) \end{gathered}\](b) 递归系统码(Recursive Systematic Code, RSC)
RSC 是 Turbo 码中采用的编码器结构,如下图所示:
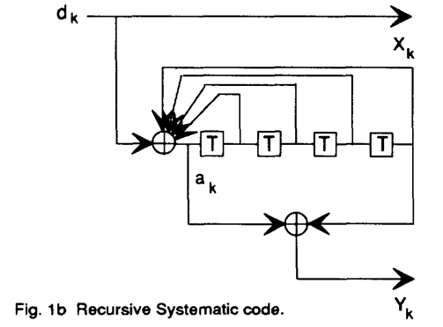
其有以下特性:
- ✅系统性:编码器输出中包含原始输入比特(称为系统比特)
- ✅递归性:编码器中包含反馈路径,输出依赖于当前输入和以往状态
相比非系统前馈码,RSC 编码器具有“记忆性”
其中 \(a_k\) 项为:
\[a_k=d_k+a_{k-1}+a_{k-2}+a_{k-3}+a_{k-4}\]- 说明:当前系统比特不仅取决于当前输入\(d_k\),还受到前几位编码输出反馈影响。
由此 \(d_k\) 可表示为:
\[d_k=a_k+a_{k-1}+a_{k-2}+a_{k-3}+a_{k-4}\]多项式表示:
\[d(D)=a(D) \cdot\left(1+D+D^2+D^3+D^4\right)\]校验比特 \(y_k\) 输出:
\[y_k = a_k+ a_{k-4}\]其多项式表示:
\[y(D)=a(D) \cdot\left(1+D^4\right)\]联立得到:
\[\frac{y(D)}{d(D)}=\frac{1+D^4}{1+D+D^2+D^3+D^4}\]于是 Turbo 编码器的生成多项式可写为:
\[g(D)=\left(1, \frac{1+D^4}{1+D+D^2+D^3+D^4}\right)\]这里的两个分量含义为:
- 第一项1:系统比特(直接输出);
- 第二项:校验比特(经过递归滤波器处理的编码输出)。
也可以使用八进制记法:
\[G_1=37, G_2=21\]3. Turbo码的并行级联结构方案
核心思想:用两个相同的递归系统卷积编码器(RSC)进行并行编码
如下图:
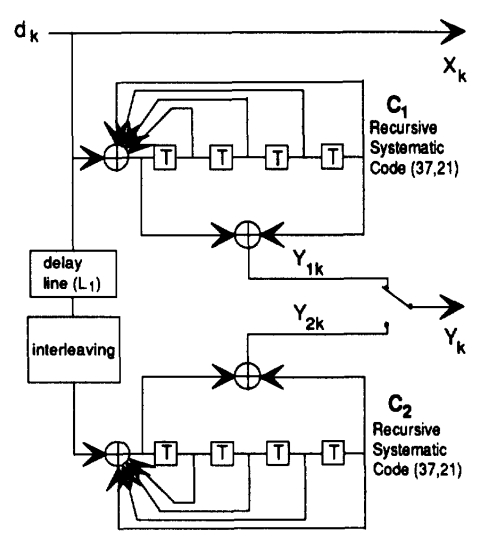
(a) 输入输出说明
🔁 输入:
- 编码器 C₁:原始序列 \(d_k\)
- 编码器 C₂:经过交织器(Interleaver)后的序列 \(\pi(d_k)\)
🧩 输出:
- 系统位(即原始信息直接输出):
- 校验位 1(基于原始序列):
- 校验位 2(基于交织后的序列):
(b) 交织器(Interleaver)的作用
在两个编码器之间插入交织器,打乱输入数据顺序后再输入第二个编码器;
目的如下:
- 增强码的分集性(diversity)
- 使得两个编码器对同一比特看到不同上下文;
- 在译码时通过多路径冗余交织结构进行更强纠错;
- 提高低权重码字的最小距离等。
原生 TURBO 编码的码率为 1/3。包含一个系统位和两个校验位。
4. TURBO 码译码机制(简要介绍)
Turbo码之所以得名,源于它的类涡轮增压译码结构,通过多个子译码器之间的信息交换与反复优化,不断改进“译码输出”,最终逼近香农极限。
(a) 译码器结构与流程
Turbo译码器由两个分量译码器组成(对应两个并行RSC编码器),并通过软信息交织反馈进行多轮迭代优化。
每次迭代包括以下步骤:
- 软输入软输出译码器:
- 输入:接收信号的对数似然比(LLR)
- 输出:对每个比特估计的新LLR
- 信息交换与交织:
- 每个译码器将其软输出通过交织器/反交织器送给另一个译码器作为先验信息
- 重复迭代(典型迭代次数:4~8次)
(b) BCJR 算法族
BCJR 算法用于 Turbo 译码中的软输入软输出概率计算,其核心目标是计算比特后验概率(LLR),属于最大后验概率(MAP)方法。
常用两种实现:
- Log-MAP:
- 精确实现 BCJR 算法的对数域版本
- 精度高,复杂度适中
- Max-Log-MAP:
- Log-MAP 的近似简化版本
- 将加法 log-sum-exp 近似为最大值,降低复杂度
- 通常译码性能略有损失,但效率更高
(c) 外信息交换算法
- 两个子译码器不断交换“概率信息”(软判决结果):
- 本轮输出 = 来自通道的观测 + 来自另一译码器的先验
- 每次迭代都能“逼近最优解”,逐渐收敛至正确码字
- 通常迭代 4~8 次就可达到较好性能(MATLAB默认 5 次)
5. MATLAB 仿真
(a) TURBO 编解码
本节评估 Turbo 编码在 AWGN 信道下的性能,并分析其在不同信噪比下的误码率表现。
TIPS:
需要根据调制阶数和码率,将Eb/N0转换为符号信噪比,对应的噪声方差产生相应复数噪声并叠加在调制信号上。
完整代码如下:
clc; clear;
% 仿真参数
EbN0_dB = 0:0.1:4; % Eb/N0范围 (dB)
numBits = 1e6; % 每个SNR仿真的比特数
maxIter = 5; % Turbo译码迭代次数
M = 16;
k = log2(M);
% 初始化
ber = zeros(size(EbN0_dB));
% Turbo码参数(LTE标准中为R=1/3)
K = 6144; % 码长
for snrIdx = 1:length(EbN0_dB)
numErrs = 0; numTotal = 0;
EbN0 = EbN0_dB(snrIdx);
fprintf('Simulating Eb/N0 = %.1f dB...\n', EbN0);
while numTotal < numBits
% ====== 1. 随机比特 ======
dataIn = randi([0 1], K, 1);
% ====== 2. Turbo 编码 ======
dataEnc = lteTurboEncode(dataIn);
% ====== 3. QPSK 调制 ======
% txSymbols = 1 - 2*double(dataEnc); % BPSK: 0 -> +1, 1 -> -1
txSymbols = lteSymbolModulate(dataEnc,'QPSK');
txSymbols2 = qammod(dataEnc, M, 'InputType','bit','UnitAveragePower',true);
% ====== 4. AWGN信道 ======
R = 1/3; % Turbo码率
EsN0 = EbN0 + 10*log10(k/3); % 转换到Es/N0
SNR = 10^(EsN0/10);
noiseVar = 1/(2*SNR);
noise = sqrt(noiseVar) * (randn(size(txSymbols)) + 1i*randn(size(txSymbols)));
rxSymbols = awgn(txSymbols,EsN0,'measured');
% rxSymbols2 = txSymbols2 + noise;
rxSymbols2 = awgn(txSymbols2,EsN0,'measured');
% signal_power = mean(abs(txSymbols2).^2); % 发射信号功率
% noise_power = mean(abs(rxSymbols2 - txSymbols2).^2); % 差值 = 噪声估计
%
% SNR_est_linear = signal_power / noise_power;
% SNR_est_dB = 10 * log10(SNR_est_linear)
% ====== 5. 软解调 ======
softBits = lteSymbolDemodulate(rxSymbols,'QPSK','Soft');
softBits2 = qamdemod(rxSymbols2, M,'OutputType','approxllr', ...
'UnitAveragePower',true,'NoiseVariance',noiseVar);
softBits2 = softBits2*(-1);
% ====== 6. Turbo译码 ======
% llrInput = 2 * rxSymbols / noiseVar;
dataOut = lteTurboDecode(softBits2, maxIter);
% ====== 7. 错误统计 ======
numErrs = numErrs + sum(dataOut ~= dataIn);
numTotal = numTotal + length(dataIn);
end
% BER计算
ber(snrIdx) = numErrs / numTotal;
end
figure
% ====== 绘图 ======
semilogy(EbN0_dB, ber, 'o-', 'LineWidth', 2); grid on;
xlabel('E_b/N_0 (dB)'); ylabel('Bit Error Rate (BER)');
title(sprintf('Turbo编码(LTE标准) - MaxLog-MAP, %d次迭代', maxIter));
legend('Turbo码 (1/3)', 'Location', 'southwest');
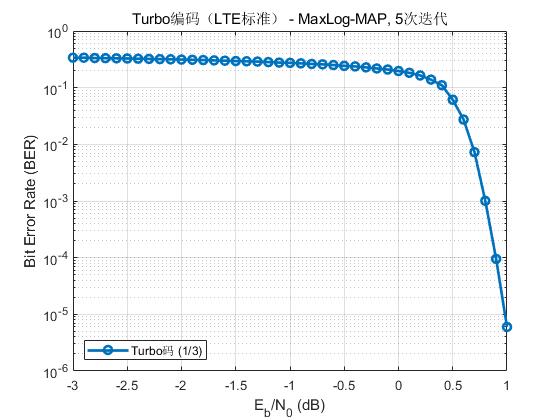
下图给出QPSK调制下,TURBO链路BER曲线:
(b) Turbo码与卷积码误码性能对比仿真
不同 SNR(Eb/N0)条件下,分别统计 Turbo 和卷积编码系统在软判决与硬判决下的 BER(误码率)。
%% TURBO 码和 卷积码对比
clear; close all;
rng default
M = 4; % QPSK
k = log2(M); % Bits per symbol
EbNoVec = (-3:6)'; % Eb/No values (dB)
numSymPerFrame = 2016; % Bits per frame
rate = 1/3; % Turbo/Conv 编码率
tbl = 32; % traceback depth for Viterbi
trellis = poly2trellis(7,[171 133 165]); % 卷积编码
% 初始化 BER 统计
berTurboSoft = zeros(size(EbNoVec));
berTurboHard = zeros(size(EbNoVec));
berConvSoft = zeros(size(EbNoVec));
berConvHard = zeros(size(EbNoVec));
h = waitbar(0, 'Running simulation...');
for n = 1:length(EbNoVec)
snrdB = EbNoVec(n) + 10*log10(k*rate);
noiseVar = 10^(-snrdB/10);
[errTurboSoft, errTurboHard, errConvSoft, errConvHard, totalBits] = deal(0);
waitbar(n/length(EbNoVec), h, ...
sprintf('Simulating: Eb/N0 = %d dB (%.0f%%)', EbNoVec(n), 100*n/length(EbNoVec)));
while errTurboSoft < 100 && totalBits < 1e6
% 1. 原始比特
dataIn = randi([0 1], numSymPerFrame, 1);
%% --- Turbo编码 ---
dataTurboEnc = lteTurboEncode(dataIn);
% QAM调制
txTurbo = qammod(dataTurboEnc,M,'InputType','bit','UnitAveragePower',true);
rxTurbo = awgn(txTurbo, snrdB, 'measured');
% 硬判决解调
rxHardTurbo = qamdemod(rxTurbo, M, 'OutputType','bit','UnitAveragePower',true);
rxHardTurboMapped = rxHardTurbo * -2 + 1; % 映射为 ±1
rxHardTurboMapped = -rxHardTurboMapped; % 翻转符号用于一致性
% 软判决解调
rxSoftTurbo = qamdemod(rxTurbo, M, 'OutputType','approxllr', ...
'UnitAveragePower', true, 'NoiseVariance', noiseVar);
rxSoftTurbo = -rxSoftTurbo;
% Turbo译码
dataTurboDecSoft = lteTurboDecode(rxSoftTurbo, 5);
dataTurboDecHard = lteTurboDecode(rxHardTurboMapped, 5);
errTurboSoft = errTurboSoft + sum(dataIn ~= dataTurboDecSoft);
errTurboHard = errTurboHard + sum(dataIn ~= dataTurboDecHard);
%% --- 卷积编码 ---
dataConvEnc = convenc(dataIn, trellis);
% QAM调制
txConv = qammod(dataConvEnc,M,'InputType','bit','UnitAveragePower',true);
rxConv = awgn(txConv, snrdB, 'measured');
% rxConv = txConv;
% 硬判决解调
rxHard = qamdemod(rxConv,M,'OutputType','bit','UnitAveragePower',true);
dataConvHard = vitdec(rxHard, trellis, tbl, 'cont', 'hard');
errConvHard = errConvHard + sum(dataIn(1:end-tbl) ~= dataConvHard(tbl+1:end));
% 软判决解调
rxSoft = qamdemod(rxConv,M,'OutputType','approxllr','UnitAveragePower',true,'NoiseVariance',noiseVar);
dataConvSoft = vitdec(rxSoft, trellis, tbl, 'cont', 'unquant');
errConvSoft = errConvSoft + sum(dataIn(1:end-tbl) ~= dataConvSoft(tbl+1:end));
totalBits = totalBits + numSymPerFrame;
end
% 存储结果
berTurboSoft(n) = errTurboSoft / totalBits;
berTurboHard(n) = errTurboHard / totalBits;
berConvSoft(n) = errConvSoft / (totalBits - tbl);
berConvHard(n) = errConvHard / (totalBits - tbl);
fprintf('Eb/N0 = %2d dB: TurboSoft = %.3e, TurboHard = %.3e, ConvSoft = %.3e, ConvHard = %.3e\n', ...
EbNoVec(n), berTurboSoft(n), berTurboHard(n), berConvSoft(n), berConvHard(n));
end
close(h);
%% 绘图对比
figure; semilogy(EbNoVec, berTurboSoft, '-o', 'LineWidth', 2); hold on;
semilogy(EbNoVec, berTurboHard, '-d', 'LineWidth', 2);
semilogy(EbNoVec, berConvSoft, '-s', 'LineWidth', 2);
semilogy(EbNoVec, berConvHard, '-^', 'LineWidth', 2);
semilogy(EbNoVec,berawgn(EbNoVec,'qam',M),'LineWidth', 2);
grid on; xlabel('E_b/N_0 (dB)'); ylabel('BER');
legend('Turbo (Soft)','Turbo (Hard)','Conv (Soft)','Conv (Hard)','Uncoded');
title('BER Comparison: Turbo vs Convolutional (Soft/Hard Decision)');
下图给出QPSK调制下的对比曲线:
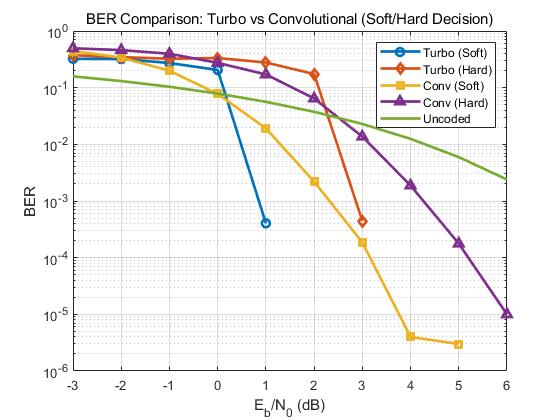
(c) 译码次数迭代仿真
上述代码易改成译码迭代次数对比仿真框架,如下所示:
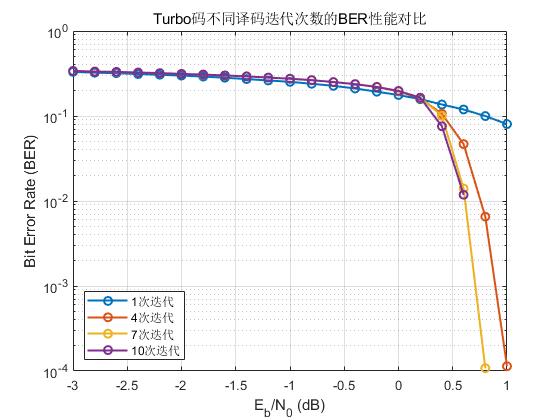
(d) 不同调制方式下的Turbo性能对比
进一步将仿真维度切换为不同调制方式(QPSK、16QAM、64QAM)
需要注意的是不同调制阶数在仿真时应使用不同的SNR区间。
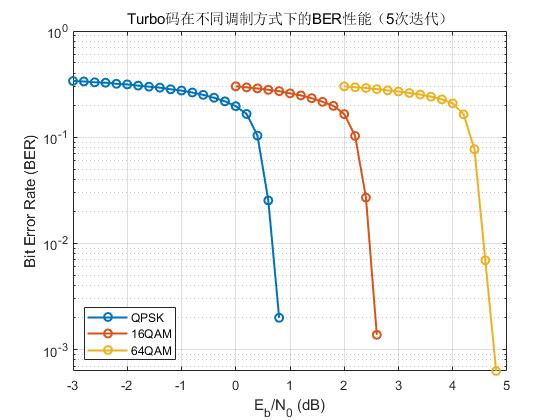
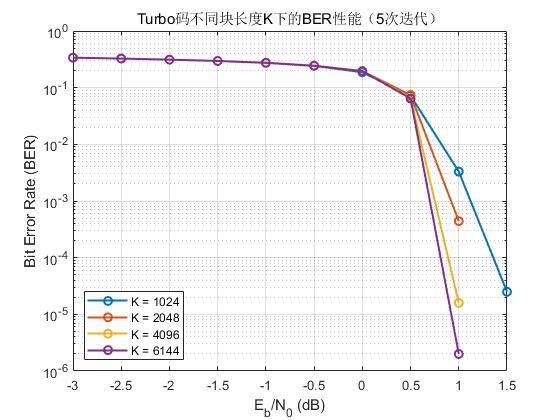
(e) 不同块长(K)对Turbo性能的影响
以下为不同块长度 K 仿真,以分析 Turbo码块长(帧长)对误码率的影响。
三、LDPC 码
1. 概述
LDPC(Low Density Parity Check Code,低密度奇偶校验码)由 Robert G. Gallager 于 1963 年首次提出。
核心特性:
- 低密度性:
奇偶校验矩阵(Parity-Check Matrix)中非零元素极少(通常小于 5%),有助于降低编码解码复杂度,便于并行处理。
- 接近香农极限:
性能接近信道容量,尤其在 5G 等高速通信系统中被广泛采用。
- 高吞吐量:
支持并行解码结构,可结合 GPU / FPGA 实现,满足高速通信需求。
- 灵活构造:
可灵活设计奇偶校验矩阵,提升适应性与性能。
2. 编码原理
🔸 校验矩阵定义
设 LDPC 校验矩阵为一个 𝑚×𝑛 的二进制稀疏矩阵 𝐻,编码后的字 𝑐 需满足:
\[H \cdot \mathbf{c}^T=0\]🔸 码字构成
LDPC 为系统码,码字 \(\mathbf{c}\) 由系统位(信息位) \(\mathbf{u}\) 和校验位 \(\mathbf{p}\) 构成:
\[\mathbf{c}=[\mathbf{u} \mathbf{~ p}]\]🔸 构造生成矩阵
若校验矩阵 𝐻 可分块写作:
\[G=\left[I \mid\left(H_1 H_2^{-1}\right)^T\right]\]🔸 编码公式
则编码过程可记为:
\[\mathbf{c}=\mathbf{u} G\]3. 具体例子
以下通过一个具体例子解释LDPC码的奇偶校验约束及其矩阵表示方式,并介绍编码的具体过程。
(a) LDPC 校验关系
🔹 奇偶校验约束
假设该 LDPC 要求所有码字 \(\mathbf{c}=\left[c_1, c_2, \ldots, c_n\right]\) 满足一组异或校验关系,即:
\[\left\{\begin{array}{l} c_1 \oplus c_2 \oplus c_4=0 \\ c_2 \oplus c_3 \oplus c_5=0 \\ c_1 \oplus c_2 \oplus c_3 \oplus c_6=0 \end{array}\right.\]🔹 矩阵表示形式
上述约束关系可表示为一个稀疏的校验矩阵 𝐻,并以矩阵形式表示:
\[H \cdot \mathbf{c}^T=0\]对应矩阵形式为:
\[H=\left[\begin{array}{llllll} 1 & 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 & 0 \\ 1 & 1 & 1 & 0 & 0 & 1 \end{array}\right]\] \[\mathbf{c}^T=\left[\begin{array}{l} c_1 \\ c_2 \\ c_3 \\ c_4 \\ c_5 \\ c_6 \end{array}\right] \quad \Rightarrow \quad H \cdot \mathbf{c}^T=\left[\begin{array}{l} 0 \\ 0 \\ 0 \end{array}\right]\]例如给定码字:
\[\mathbf{c}=\left[\begin{array}{llllll} 1 & 1 & 0 & 0 & 1 & 0 \end{array}\right]\]满足约束条件:
\[\begin{aligned} & 1 \oplus 1 \oplus 0=0 \\ & 1 \oplus 0 \oplus 1=0 \\ & 1 \oplus 1 \oplus 0 \oplus 0=0 \end{aligned}\](b) 编码过程
以上介绍了 LDPC 的校验关系,目的是解释 LDPC 码字应该满足什么条件。
下面讲介绍:
🔹 已知信息比特,如何求出校验比特
设已知前 3 位信息比特\(u=\left[c_1, c_2, c_3\right]=[1,1,0]\),目标是根据校验矩阵 𝐻 的约束求出校验比特 \(\left[c_4, c_5, c_6\right]\)
根据之前的奇偶校验约束:
\[\left\{\begin{array}{l} c_1 \oplus c_2 \oplus c_4=0 \Rightarrow c_4=c_1 \oplus c_2=1 \oplus 1=0 \\ c_2 \oplus c_3 \oplus c_5=0 \Rightarrow c_5=c_2 \oplus c_3=1 \oplus 0=1 \\ c_1 \oplus c_2 \oplus c_3 \oplus c_6=0 \Rightarrow c_6=c_1 \oplus c_2 \oplus c_3=1 \oplus 1 \oplus 0=0 \end{array}\right.\]由此可以手动求出完整码字:
\[\mathbf{c}=\left[c_1, c_2, c_3, c_4, c_5, c_6\right]=[1,1,0,0,1,0]\]🔹 编码的两种等价表示
✅ 1. 校验矩阵约束(H):
上文已经提及,码字要满足:
\[H \cdot \mathbf{c}^T=0\]✅ 2. 生成矩阵法(G):
由信息比特向量,通过生成矩阵 𝐺 得到完整码字:
\[\mathbf{c}=u \cdot G\]由前文校验矩阵可以求得生成矩阵 𝐺 为:
(有关校验矩阵和生成矩阵的关系将在下节介绍)
\[G=\left[\begin{array}{llllll} 1 & 0 & 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 0 & 1 & 1 \end{array}\right]\]编码过程即:
\[\mathbf{c}=\left[\begin{array}{lll} 1 & 1 & 0 \end{array}\right] \cdot G=\left[\begin{array}{llllll} 1 & 1 & 0 & 0 & 1 & 0 \end{array}\right]\]🔹 小结
- 校验矩阵 H 和 生成矩阵 G 是同一 LDPC 编码方案的两种数学表示。
- 从公式上看:校验矩阵用于约束条件(译码),生成矩阵用于编码计算。
(c) 校验矩阵和生成矩阵
有了校验矩阵 𝐻,但怎么构造生成矩阵 𝐺 呢?
在 LDPC 编码中,校验矩阵 𝐻 是编码设计的起点,它定义了码字必须满足的奇偶校验约束:
\[H \cdot c^T=0\]而为了完成编码,我们需要构造生成矩阵 𝐺,使得:
\[c=u \cdot G\]其中 𝑢 是信息比特,𝑐 是完整码字,且必须满足校验约束。
设 𝐻 是 𝑚×𝑛 的矩阵,码字长度 𝑛,信息位个数 𝑘=𝑛−𝑚。
希望通过线性代数方法构造 𝐺。方法如下:
步骤一:将 𝐻 转化为系统形式(Systematic Form)
可通过高斯消元法将其行变换成系统形式,将 𝐻 分成两部分:
\[H=\left[\begin{array}{ll} H_1 & H_2 \end{array}\right] \quad \text { 其中: } H_1 \in \mathbb{F}_2^{m \times k}, \quad H_2 \in \mathbb{F}_2^{m \times m}\]要求:𝐻2 可逆(设计时强制满足)
步骤二:构造生成矩阵 𝐺
对应生成矩阵为:
\[G=\left[I_k \mid\left(H_1 H_2^{-1}\right)^T\right]\]前面是 𝑘×𝑘 单位矩阵,后半部分为奇偶校验部分的“补偿项”。
步骤三:编码过程
信息位\(u \in \mathbb{F}_2^{1 \times k}\),码字\(c \in \mathbb{F}_2^{1 \times n}\) ,编码过程:
\[c=u \cdot G\]✅ 回看前面的例子:
假设已知:
\[H=\left[\begin{array}{llllll} 1 & 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 & 0 \\ 1 & 1 & 1 & 0 & 0 & 1 \end{array}\right]=[\underbrace{\left[\begin{array}{lll} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right]}_{H_1} \underbrace{\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]}_{H_2}]\]则:
\[G=\left[I_3 \mid\left(H_1 H_2^{-1}\right)^T\right]=\left[I_3 \mid H_1^T\right]=\left[\begin{array}{cccccc} 1 & 0 & 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 0 & 1 & 1 \end{array}\right]\](d) MATLAB 验证示例
以下 MATLAB 代码实现了上述构造和验证过程:
clc; clear;
% Step 1: 定义校验矩阵 H(在GF(2)中)
H = gf([
1 1 0 1 0 0;
0 1 1 0 1 0;
1 1 1 0 0 1
], 1); % GF(2)
% Step 2: 拆分 H1 和 H2(H = [H1 | H2])
H1 = H(:, 1:3);
H2 = H(:, 4:6);
% Step 3: 求 H2 的逆
H2_inv = inv(H2); % 逆矩阵
% Step 4: 构造生成矩阵 G = [I | (H1 * H2^-1)^T]
G = [eye(3), (H1 * H2_inv).'];
% temp = G*H.';
% disp(temp.x);
disp('生成矩阵 G = ');
disp(G.x); % 提取原始二进制矩阵显示
% Step 5: 给定信息比特 u
u = gf([1 1 0], 1); % c1, c2, c3
% Step 6: 编码 c = u * G
c = u * G;
disp('编码得到的码字 c = ');
disp(c.x); % 显示为普通二进制数
% Step 7: 校验:H * c^T 应为全零向量
check = H * c.';
disp('校验结果 H * c^T = ');
disp(check.x); % 应该为 [0; 0; 0]
需要注意的是:
- 所有运算必须在 GF(2) 上进行(逻辑异或 + 与);
- 校验矩阵 𝐻 决定校验关系,生成矩阵 𝐺 决定编码规则,但两者本质一样。
4. LDPC 解码介绍(简要说明)
LDPC 解码的核心思想是:
根据校验矩阵 𝐻,利用接收信号的信息,反复迭代逼近满足所有校验条件的码字。
🔹 解码目标
已知:
- 接收端获得的软信息(如 LLR 值);
- LDPC 校验矩阵 𝐻。
解码器需要从中恢复出原始信息比特 𝑢,使得输出码字 𝑐 满足:
\[H \cdot c^T=0\]🔹 主流解码算法
✅ BP 算法(Belief Propagation,置信传播)
- 基于 Tanner 图;
- 在校验节点与变量节点之间反复传递信息;
- 迭代更新每一比特的“置信度”(如 LLR)直到收敛。
✅ Min-Sum 算法(简化版 BP)
- 将 BP 中复杂的 tanh 运算简化为 min 操作;
- 性能略低于 BP,但复杂度更低,易于硬件实现。
5. MATLAB 仿真验证
(a) LDPC 编解码
本节展示一个完整的基于 5G NR 标准 LDPC 编解码的蒙特卡洛仿真过程,统计不同信噪比下的比特误码率(BER)。本例采用:
- Base Graph 1 (BGN=1)
- QPSK 调制
- AWGN信道
clc; clear;
% ==== 参数设置 ====
EbN0_dB = -2:0.2:3; % Eb/N0范围
numBitsPerSNR = 1e6; % 每个SNR下模拟的比特数
maxIter = 22; % LDPC最大译码迭代次数
modType = 'QPSK'; % 调制方式
M = 4; k = log2(M); % 每符号bit数
% LDPC参数(5G NR Base Graph 2)
bit_len = 22*288;
bgn = 1; % Base graph number
R = 1/3; % 实际码率
ber = zeros(size(EbN0_dB)); % 初始化BER结果
for snrIdx = 1:length(EbN0_dB)
EbN0 = EbN0_dB(snrIdx);
numErrs = 0; numTotal = 0;
fprintf('Simulating Eb/N0 = %.1f dB...\n', EbN0);
while numTotal < numBitsPerSNR
% ==== 1. 生成原始数据(含填充) ====
data = randi([0 1], bit_len, 1); % 信息比特
%txcbs = [data; -1*ones(F,1)]; % 添加filler
% ==== 2. LDPC编码 ====
codeword = nrLDPCEncode(data, bgn);
% ==== 3. QPSK调制 ====
modSig = qammod(codeword, M, 'InputType','bit','UnitAveragePower',true);
% ==== 4. AWGN信道 ====
EsN0 = EbN0 + 10*log10(k*R); % 转换为符号能量比
SNR = 10^(EsN0/10);
noiseVar = 1/(2*SNR); % 复高斯每维噪声功率
rxSig = awgn(modSig, EsN0, 'measured');
% ==== 5. 软解调 ====
llr = qamdemod(rxSig, M,'OutputType','approxllr', ...
'UnitAveragePower',true,'NoiseVariance',noiseVar);
% ==== 6. LDPC译码 ====
decoded = nrLDPCDecode(llr, bgn, maxIter);
% ==== 7. 填充位对齐为0,进行比特比较 ====
txCompare = data;
numErrs = numErrs + sum(decoded ~= txCompare);
numTotal = numTotal + bit_len;
end
ber(snrIdx) = numErrs / numTotal;
end
% ==== 绘图 ====
figure;
semilogy(EbN0_dB, ber, 'o-', 'LineWidth', 2); grid on;
xlabel('E_b/N_0 (dB)'); ylabel('Bit Error Rate (BER)');
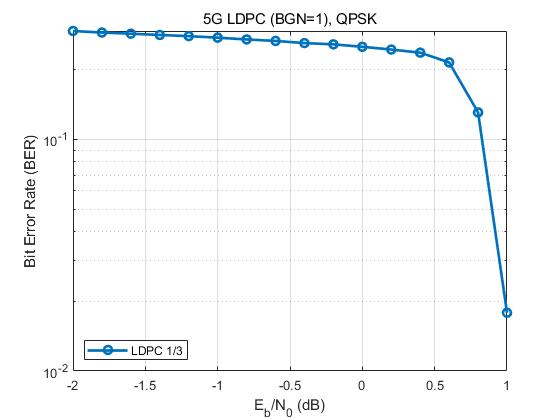
title(sprintf('5G LDPC (BGN=%d), QPSK', bgn));
legend('LDPC 1/3', 'Location', 'southwest');
📌 关于仿真中码长的说明
在 5G NR LDPC 编码中,信息块长度 𝐾 通常需要从一组标准允许的取值集合中选取,否则会涉及:
- Filler bits(填充比特)插入:将无效位置填为 -1
- LLR 对应位置置零:解调后需手动屏蔽 filler 位影响
- 对比误码时需剔除 filler 区,否则统计不准确
本仿真中的处理方式:避免补零,直接选合法块长,使用这些标准值可避免补齐 filler 等操作。
仿真结果如下:
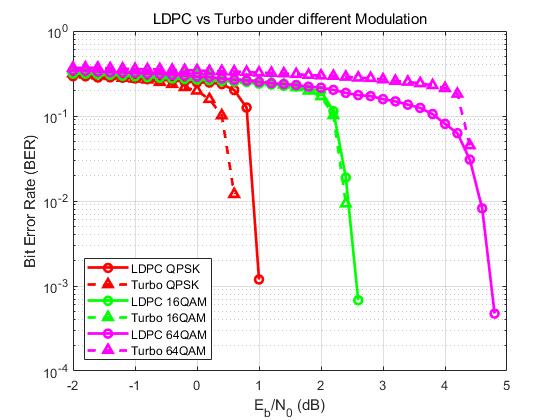
(b) LDPC VS TURBO
仿真对比LDPC和TURBO的性能对比。Turbo 和 LDPC 的性能比较接近:
四、总结
Turbo 编码和 LDPC 编码都是接近香农极限的现代信道编码方案。
Turbo 编码结构简单,适合低信噪比条件,在3G/4G中广泛应用;
而 LDPC 编码具备强大的并行处理能力,误码地板更低,更适合高速、低延迟的系统,是5G、Wi-Fi等通信标准的首选。
两者都推动了通信技术的发展,都是现代通信中不可或缺的核心编码方案,体现了强大而高效的纠错能力。
文档信息
- 本文作者:Ziyue Qi
- 本文链接:https://www.qiziyue.cn/2025/07/24/Turbo_LDPC/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)