一、引言:4G 信道编码概述
信道编码是确保可靠传输的关键技术之一。此前我们已经介绍了基本的信道编码方法,如重复码、汉明码,以及现代通信中广泛使用的 Turbo 码与 LDPC 码。它们分别代表了不同复杂度与性能水平的编码手段。
在 4G(LTE)系统中,为了同时满足高速率、低误码率和多种业务场景的需求,信道编码流程被设计成一个模块化、层次分明的结构,接下来将介绍4G系统下行信道编码过程。
二、4G下行信道编码流程总体介绍
在 LTE 系统中,下行共享信道(DL-SCH)是最主要的物理层传输信道之一,用于承载几乎所有的用户下行数据信息。
为了确保数据在无线信道中能够可靠、高效地传输,3GPP 标准(TS 36.212 Section 5.3.2)定义了一套完整而严谨的信道编码处理流程。
这一过程的目标是:
将上层传输块(Transport Block)加工为可以在无线信道中稳健传输的比特流,并兼顾纠错能力、信道利用率以及系统灵活性。
整个过程可以分为如下五个主要步骤:
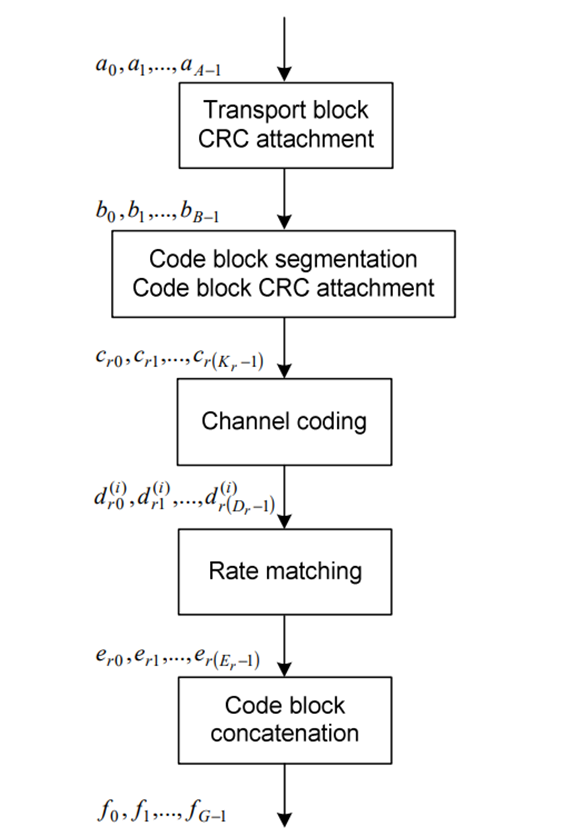
- 传输块添加CRC(Transport Block CRC attachment) 在发送数据之前,首先为每个传输块添加CRC校验码。这一步的主要目的是在接收端检测是否发生了不可恢复的传输错误。
- 如果CRC校验失败,接收端可以触发重传机制。
- CRC的引入使得物理层具备初步的错误检测能力。
- 码块分段与子块CRC附加(Code Block Segmentation & CRC) LTE 的 Turbo 编码器对输入数据长度有最大支持限制(6144 bits),因此,当传输块较大时,需要将其分段成多个子块,并且为每个子块附加CRC以确保分段后的每部分都能被独立检测。
- 信道编码(Channel Coding) 每个子块将被分别送入 Turbo 编码器进行前向纠错编码,默认采用 1/3 率的并行级联卷积码(PCCC)结构
- 速率匹配(Rate Matching) 由于Turbo编码输出的比特数量大于可用的无线资源,因此需要执行速率匹配,将编码后的比特数调整到合适的长度。
- 包括比特交织、子块循环移位和比特选择/丢弃。
- 同时支持 HARQ 多次重传与比特组合。
- 码块级联(Code Block Concatenation) 将多个子块中速率匹配后生成的比特流拼接成一个连续的输出序列,供后续调制映射使用。
三、传输块级 CRC 添加(Transport Block CRC Attachment)
在 LTE 下行传输中,物理层接收到的传输数据块(Transport Block, TB)在编码前,必须添加一个 24比特的循环冗余校验(CRC),以检测数据在整个传输过程中的完整性。
1. 传输块CRC添加
- 传输块输入:比特序列
数据按最低比特优先(LSB first)映射为最高有效位(MSB)先发,即按字节顺序排列
CRC计算与生成(基于TS 36.211 §5.1.1)
此处使用的是LTE中定义的24位的CRC24A,其生成多项式为:
\[g_{C R C 24 A}(D)=D^{24}+D^{23}+D^{18}+D^{17}+D^{14}+D^{11}+D^{10}+D^7+D^6+D^5+D^4+D^3+D+1\]- 该多项式用于对原始比特流进行模2除法,得到的24比特余数即为校验序列:
- 编码结构
CRC编码是系统式编码,即输出的编码序列由原始数据比特和CRC校验比特串联而成:
\[a_0, a_1, \ldots, a_{A-1}, p_0, p_1, \ldots, p_{23}\]2. CRC的特性与意义
CRC(循环冗余校验)特点(名字的由来):
- 冗余性:CRC校验位并不承载原始数据信息,但它提供了检测错误的能力,是可靠通信不可或缺的手段;
- 循环性:CRC利用数据比特进行循环移位与模2运算,是进行检验的方法和具体操作路径。
3. 附录:CRC编码的基本原理(前置知识补充)
CRC(Cyclic Redundancy Check) 是一种广泛使用的差错检测技术,其核心思路是:
- 利用多项式生成规则对原始数据进行处理;
- 生成一段用于校验的冗余比特(校验位);
- 在接收端重新计算CRC并与接收到的CRC比对,以判断是否发生差错。
(a) CRC 的数学基础
CRC 编码的本质是:
在 GF(2) 上,将输入数据比特序列视为一个多项式,用预定义的生成多项式进行模 2 除法,得到余数即为 CRC 校验位。
- GF(2) 是一个二元有限域,仅有 0 和 1,运算规则为模 2 加减。
- 每一比特视为一个多项式的系数,例如序列:
可表示为:
\[a_0+a_1 D+a_2 D^2+\cdots+a_{A-1} D^{A-1}\](b) 以 CRC24A 为例说明系统编码形式
在 LTE 中,使用 CRC24A 生成 24 位校验,形成如下系统编码:
- 生成多项式为:
- 编码后多项式:
- 最终编码序列为:
(c) 发送端如何生成 CRC
- 补 0:向输入比特流后添加 24 个零(CRC多项式的阶数减去1的长度),比特数扩展至至 𝐴+24
- 整除运算:用生成多项式整除这个扩展序列,取余数
- 校验位拼接:将余数作为校验位附加在原始数据后
(d) 接收端如何验证 CRC
接收端将收到的“原始数据 + CRC”视为一个整体多项式,使用同样的生成多项式再次进行除法:
- 若余数为 0 → 校验通过
- 若余数非 0 → 检测到错误
(e) MATLAB 验证
下面通过 MATLAB 验证CRC 编码与校验原理:
- 数据发送端的 CRC 附加过程;
- 数据接收端的 CRC 校验过程;
- 错误注入以验证 CRC 检错能力。
主要代码:
for i = 1:length(dataBits)
bit = dataBits(i);
feedback = xor(bit, reg(1));
reg = [reg(2:end), 0]; % 左移一位
if feedback
reg = xor(reg, poly(2:end)); % 异或多项式(去掉最高位)
end
end
CRC中的模2多项式除法,即 GF(2) 上的带余除法,其本质和函数 gfdeconv() 做的是一回事。
模2除法过程等价于移位寄存器逻辑:
- 初始化
reg = zeros(1, crc_len);
表示寄存器当前为 0,此处相当于余数初始为 0。
- 遍历每一个输入比特:
bit = dataBits(i);
feedback = xor(bit, reg(1));
将当前数据位与“当前最高位(最高次幂)”做异或。
如果为1,表示当前位需要“除一次” → 也就是要执行一次 XOR 多项式减法。
- 左移一位:
reg = [reg(2:end), 0];
模拟除法过程的“移位”,相当于:舍弃最高位,把整个余式左移 1 位,准备容纳新的低位;
- 多项式减法(异或):
if feedback
reg = xor(reg, poly(2:end));
end
如果当前最高位是 1,则用生成多项式(去掉最高位项)对当前寄存器进行异或。
总结模拟了除法的本质过程:从高位开始逐步减去生成多项式(异或),直到低位,最终留下余数。
四、码块分割与子块 CRC 附加
LTE 中,Turbo 编码器的输入比特数存在上限(最大支持 6144 比特)。
当传输块(Transport Block)较大时,必须将其拆分为若干个更小的码块(Code Block, CB),以便逐个编码处理。
为了增强错误检测能力,每个分割后的码块还要单独附加 CRC 校验位(子块 CRC)
该步骤的作用主要是:
- 适应 Turbo 编码器输入长度限制
- 支持并行编码结构,提高编解码效率
- 提升错误检测能力,配合 HARQ
1. 输入输出说明
(a) 输入比特序列:
\[b_0, b_1, \ldots, b_{B-1}\]为前一步添加了传输块 CRC 后的序列,长度 𝐵=𝐴+24
(b) 输出码块:
分割后的序列变为 𝐾 个码块,每个码块记为:
\[\mathbf{c}_r=\left[c_{r, 0}, c_{r, 1}, \ldots, c_{r,\left(C_r-1\right)}\right]\]其中:
- 𝑟 表示码块编号(0 到 𝐾−1)
- 𝐶𝑟是第 𝑟 个码块的长度(包含24位子块CRC)
2. 码块数量计算与输出长度确定
(a) 输入参数:
- B:传输块比特长度(已添加传输块级 CRC 的结果)
- Z:Turbo 编码器最大输入长度(LTE标准中为 6144)
- 输出目标:确定分段数量 C,以及总输出长度 B′
(b) 分割规则
✅ 情况1:单个码块场景(无需分段)
如果:
\[B \leq Z\]- 不进行分段,作为一个码块处理
- 码块数目 C=1
- 不需要附加子块级 CRC
- 总输出比特数:
✅ 情况2:多个码块场景(需要分段)
如果:
\[B > Z\]- 计算出需要划分的码块数量:
其中 𝐿=24,即每个码块附加的子块 CRC 长度
- 每个码块最多有效负载为 𝑍−24
- 为每个码块附加 24 位 CRC 后,输出总长度为:
⚠️ 若 B 不能整除,则最后一个码块会使用填充位(filler bits)填满。
(c) 码块长度分配与填充位处理
当传输块被划分为多个码块(即 𝐶>1)时,需要进一步确定:
- 每个码块的实际长度
- 哪些码块需要填充比特(filler bits)
相关参数说明:
| 参数 | 含义与说明 |
|---|---|
| \(B\) | 原始数据块加传输块CRC后的长度 |
| \(C\) | 总码块数量(由上一步计算:\(C = \lceil \frac{B}{Z - 24} \rceil\)) |
| \(L\) | 子块CRC位数,固定为 24(仅 C > 1 时才添加) |
| \(B' = B + C \cdot L\) | 包含子块CRC的总输出比特数 |
| \(K_+\) | 主码块长度,从标准表格中查得(满足 \(C \cdot K_+ \geq B'\) 的最小值) |
| \(K_-\) | 次码块长度,从表格中查得(满足 \(K_- < K_+\) 的最大值) |
| \(\Delta_K = K_+ - K_-\) | 主次码块长度差 |
| \(C_-\) | 使用次码块长度 \(K_-\) 的子块数量 |
| \(C_+ = C - C_-\) | 使用主码块长度 $K_+$ 的子块数量 |
| \(F\) | 填充位数,用于将次码块前部填满到 \(K_-\) 长度,补在码块开头,不编码不映射 |
标准使用查表匹配(TS 36.212 表5.1.3-3)方式动态确定:
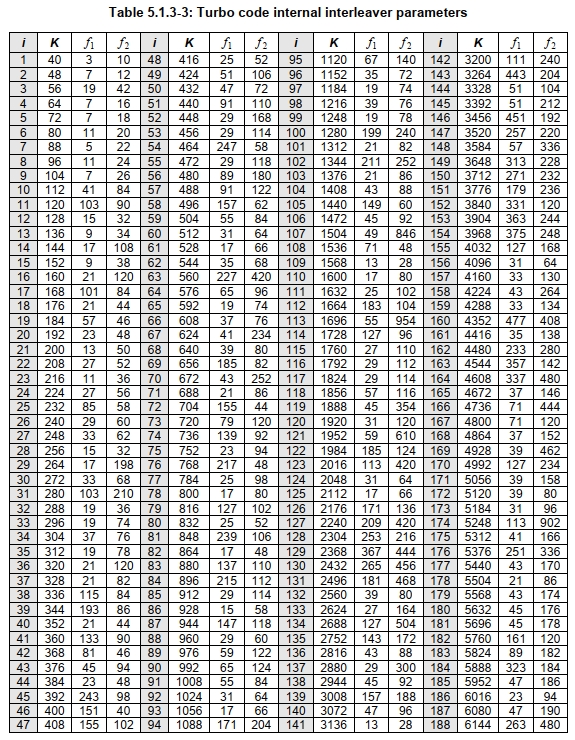
Step 1: 查表得到 𝐾+
从标准表中找到最小的 𝐾,满足:
\[C \cdot K \geq B^{\prime}\]Step 2: 查表得到 𝐾−
从标准表中找到最大 𝐾,满足:
\[K<K_{+}\]这样,可以把总比特长度拆分成若干个较长码块和若干个较短码块。
Step 3: 计算差值
\[\Delta_K=K_{+}-K_{-}\]Step 4: 计算使用次码块长度的数量:
\[C_{-}=\left\lfloor\frac{C \cdot K_{+}-B^{\prime}}{\Delta_K}\right\rfloor\]Step 5: 计算主码块数量
\[C_{+}=C-C_{-}\]Step 6: 计算填充比特数
\[F=C_{-} \cdot K_{-}+C_{+} \cdot K_{+}-B^{\prime}\]Step 7:填充比特处理(Filler Bits)
填充比特位置固定:始终出现在第一个比特之前,不参与编码与调制。写作:
\[c_{0, k}=<\text { NULL }>\quad \text { for } \quad k=0 \text { to } F-1\](d) 码块分割与填充比特计算——示例说明
假设某次传输中,编码比特长度为 12684 bits,请计算:
- 需要划分多少个码块;
- 每个码块长度是多少;
- 填充比特为多少;
- 总输出比特长度(含子块 CRC 与填充位)。
第一步:添加传输块级 CRC 得到总输入长度B
\[B=12684+24=12708\]第二步:确定是否需要分段,计算码块数量C
根据 Turbo 编码器最大支持比特数:
- Z=6144
- 每个码块附加 24 位 CRC(L = 24)
- 有效数据载荷大小 = 𝑍−24=6120
第三步:计算添加子块CRC后的总编码输入长度 𝐵′
\[B^{\prime}=B+C \cdot 24=12708+3 \cdot 24=12780\]第四步:查表获取码块长度
查 3GPP TS 36.212 表 5.1.3-3,找到满足以下条件的两个码块长度:
K+:最小满足 𝐶⋅𝐾+≥𝐵′的长度:
\[K_{+}=4288\]𝐾−:表中小于 𝐾+ 的最大值:
\[K_{-}=4224\]同时求得:
\[\Delta_K=K_{+}-K_{-}=4288-4224=64\]第五步:计算次码块数量 𝐶−
\(C_{-}=\left\lfloor\frac{3 \cdot 4288-12780}{64}\right\rfloor=\left\lfloor\frac{12864-12780}{64}\right\rfloor=\left\lfloor\frac{84}{64}\right\rfloor=1\) 第六步:计算主码块数量 𝐶+
\[C_{+}=C-C_{-}=3-1=2\]第七步:计算填充比特数量 𝐹
\(F=C_{+} \cdot K_{+}+C_{-} \cdot K_{-}-B^{\prime}=2 \cdot 4288+1 \cdot 4224-12780=12800-12780=20\)
图示说明解析
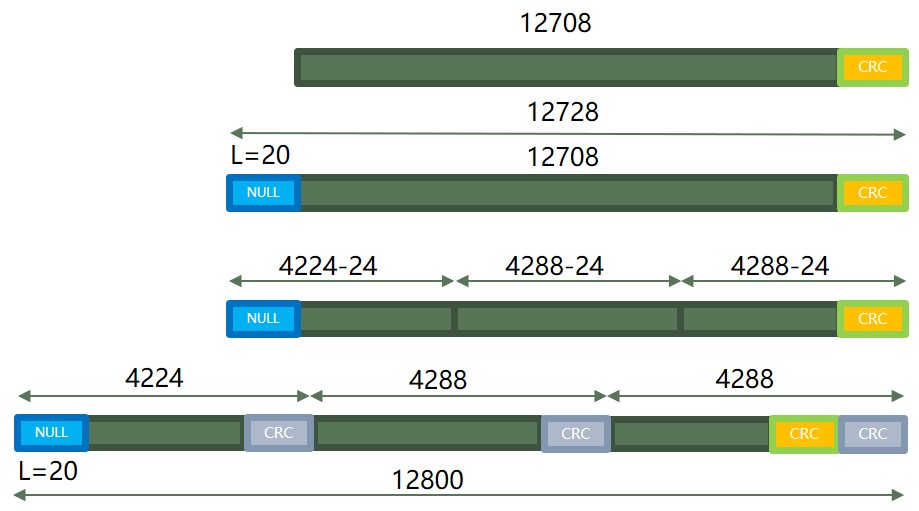
| 子块编号 | 填充 | 有效数据 | 子块 CRC | 总长度 |
|---|---|---|---|---|
| Block 0 | 20 | 4204 | 24 | 4248 |
| Block 1 | 0 | 4264 | 24 | 4288 |
| Block 2 | 0 | 4264 | 24 | 4288 |
| 合计 | 12800 |
五、信道编码 —— Turbo 编码(Channel Coding)
在完成了传输块级 CRC 添加、码块分段与子块 CRC 添加后,系统将输入比特序列切分为多个码块(Code Block, CB)。
接下来,每个码块将被独立编码,即:
每一个码块单独进入 Turbo 编码器处理,编码过程遵循 TS 36.212 第 5.1.3.2 节中的描述。
1. 输入输出结构
✅ 输入:
每个码块编号为 𝑟,其原始输入比特序列为:
\[c_{r, 0}, c_{r, 1}, \ldots, c_{r,\left(K_r-1\right)}\]其中 𝐾𝑟 是第 𝑟 个码块的总比特数(含子块 CRC 和填充比特)。
✅ 输出:
Turbo 编码器输出三条子比特流:
- 系统比特(systematic bits)即原始比特:
- 奇偶校验比特路径1(第一分支编码器):
奇偶校验比特路径2(第二分支编码器,基于交织后的数据):
\[d_i^{(2)}\]最终每个流的输出的比特数量为:
\[D_r=K_r+4\]其中附加的 4 位为 Turbo 编码尾比特(termination bits),用于保证解码器清空内部状态。
Turbo 编码通过两路独立校验链路产生冗余,极大增强了纠错能力,适用于高误码环境中的低信噪比可靠传输
2. Turbo 编码器结构
在 LTE 系统中,信道编码使用1/3 码率的 Turbo 编码器,其结构包括:
- 两个3阶递归系统卷积编码器(RSC, Recursive Systematic Convolutional Encoder)
- 一个内部交织器(Interleaver)
(a) 结构说明
结构图如下:
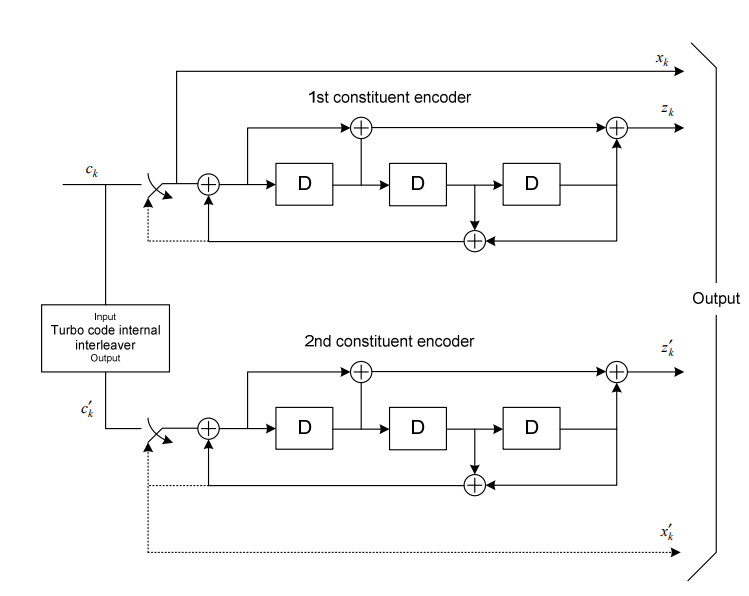
每个 RSC 编码器的传输函数为:
\[G(D)=\left[1, \frac{g_1(D)}{g_0(D)}\right]\]其中:
- 𝑔0(𝐷):反馈路径多项式,用于寄存器状态反馈
- 𝑔1(𝐷):前馈路径多项式,用于产生校验位
相关参数如下:
| 参数 | 多项式表达式 | 二进制表示(从高到低) |
|---|---|---|
| \(g_0(D)\) | \(1 + D^2 + D^3\) | 1101 |
| \(g_1(D)\) | \(1 + D + D^3\) | 1011 |
(b) 关键参数定义
✅ 第一个分支编码器
- 输入比特 𝑐𝑘 直接进入 第一个 RSC 编码器
- 编码器产生系统比特:
- 第一路径奇偶校验比特:
✅ 第二个分支编码器
- 输入比特 𝑐𝑘 经 Turbo 内部交织器 重新排列后生成:
- 进入 第二个 RSC 编码器,输出第二路校验比特:
最终输出比特为:
\[\left[x_k, z_k, z_k^{\prime}\right]\]实现码率 1/3 编码
✅ 编码器初始状态:
所有寄存器在开始时都被设置为 0,这保证每个码块独立编码,且便于尾比特清空状态。
编码器每处理一个输入比特 ,将输出三个比特,对应三个路径:
| 符号 | 含义 | 来源路径 |
|---|---|---|
| \(d_k^{(0)}\) | 直接传递的系统比特 | 原始输入 \(c_k\) |
| \(d_k^{(1)}\) | 第一路校验比特(路径1) | 第一编码器\(z_k\) |
| \(d_k^{(2)}\) | 第二路校验比特(路径2) | 第二编码器(交织后输入)\(z_k^{\prime}\) |
(c) Turbo 编码尾比特生成与网格终止
对应 TS 36.212 §5.1.3.2.2 Trellis Termination
Turbo 编码器本质上是两个RSC(递归系统卷积)编码器并行工作,这些编码器内部都有寄存器状态(Memory)。
编码结束时,这些寄存器可能仍处于“非零状态”,如果不处理,会造成译码路径不完整,影响误码率性能。
两个编码器的反馈路径上有一个“输入选择开关”;
正常编码阶段,这个开关选择的是原始输入比特
尾比特阶段,开关切换,改为由状态反馈逻辑生成的“尾比特驱动输入”,用于清空缓存状态、逐步驱动状态机走回原点。
以下是三个流 4bit 尾比特输出:
\[\begin{aligned} &d_K^{(0)}=x_K, d_{K+1}^{(0)}=z_{K+1}, d_{K+2}^{(0)}=x_K^{\prime}, d_{K+3}^{(0)}=z_{K+1}^{\prime}\\ &d_K^{(1)}=z_K, d_{K+1}^{(1)}=x_{K+2}, d_{K+2}^{(1)}=z_K^{\prime}, d_{K+3}^{(1)}=x_{K+2}^{\prime}\\ &d_K^{(2)}=x_{K+1}, d_{K+1}^{(2)}=z_{K+2}, d_{K+2}^{(2)}=x_{K+1}^{\prime}, d_{K+3}^{(2)}=z_{K+2}^{\prime} \end{aligned}\](d) Turbo编码器内部交织器
对应 3GPP TS 36.211 §5.1.3.2.3
目的在于,将原始比特序列重新打乱重排,使得突发错误转化为随机错误,增强 Turbo 编码的纠错性能。
Turbo 编码器使用一种固定算法型交织器,规则如下:
\[\Pi(i)=\left(f_1 \cdot i+f_2 \cdot i^2\right) \quad \bmod K\]| 符号 | 含义 |
|---|---|
| \(i\) | 输入序列的位置 |
| \(\Pi(i)\) | 该输入比特在交织后被放置的位置(输出位置) |
| \(f_1, f_2\) | 由码块长度 𝐾 决定的固定参数,查表得到 |
| \(K\) | 码块长度 |
交织器参数查表如下:

例如:
假设码块长度 𝐾=40,查得:
\[f_1 = 3, f_2 = 40\]若要计算交织后第 5 个比特来自原始输入序列中哪一位:
\[\Pi(5)=\left(3 \cdot 5+10 \cdot 5^2\right) \bmod 40=(15+250) \bmod 40=265 \bmod 40=25\]即:输出第 5 位来自输入第 25 位的比特。
六、速率匹配(Rate Matching)
此步骤位于 Turbo 编码之后,目的是将 Turbo 编码的输出序列调整为适配不同信道传输容量的目标比特数。
三大组件:
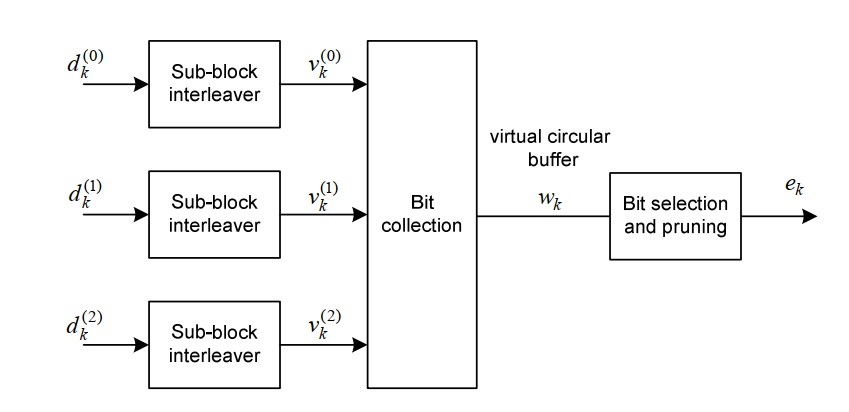
- 子块交织(Sub-block Interleaver)
将 Turbo 输出的三个流分别交织,打乱顺序,分散错误。
- 比特收集(Bit Collection):
三路交织输出被合并为一个虚拟循环缓冲区(virtual circular buffer),用于统一排布所有比特位。
- 比特选择与修剪(Bit Selection & Pruning):
从缓冲区中提取目标个数的比特输出,形成最终用于调制映射的比特序列。
1. 子块交织(Sub-block Interleaver)
标准参考:TS 36.211 §5.1.4.1.1
子块交织器的作用是将输入比特按照行列交织规则重新排列,打乱原始顺序,实现如下两大目标:
- 抗突发错误:
通过打乱相邻比特在时间上的顺序,可将连续错误分散到不同位置,提高译码器恢复能力。
- 适配后续速率匹配模块:
为速率匹配中的“虚拟循环缓冲区”提供结构化输入,简化后续比特选择与修剪操作。
📌 Turbo码输出的前两个比特流的交织处理
即:
系统位 \(d_k^{(0)}\)和第一个校验位流\(d_k^{(1)}\)
第一步:构建填充矩阵
- 按照标准,交织矩阵列数取固定值:
- 行数计算(向上取整):
其中 𝐷 是一个子块交织器的输入长度; 若不足 𝑅×𝐶 个元素,尾部补 NULL(空比特)
- 原始矩阵填充(按行写入):
第二步:列间置换
- 标准给出置换表(表 5.1.4-1):
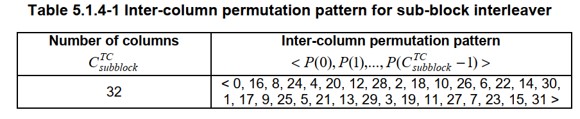
将原矩阵的列索引 𝑗 映射为 𝑃(𝑗),形成置换矩阵
\[Y_{\text {permuted }}=\left[\begin{array}{cccc} y_{P(0)} & y_{P(1)} & \cdots & y_{P(31)} \\ y_{P(0)+32} & y_{P(1)+32} & \cdots & y_{P(31)+32} \\ \vdots & \vdots & \ddots & \vdots \\ y_{P(0)+32(R-1)} & y_{P(1)+32(R-1)} & \cdots & y_{P(31)+32(R-1)} \end{array}\right]\]第三步:按列优先顺序输出
输出比特的第 𝑘 个位置为:
\[v_k=y_{P(j)+C_{\text {subblock }}^{\mathrm{TC}} \cdot r}\]其中:
\(j=\left\lfloor\frac{k}{R_{\text {subblock }}^{\mathrm{TC}}}\right\rfloor\) \(r=k \bmod R_{\text {subblock }}^{\mathrm{TC}}\)
📌 第三个输出流的交织处理
与前两个交织器一样,经过填充矩阵、列间置换、按列读取输出。
第三个交织器的输出序列与前两个不同,采用如下公式:
\[v_k^{(2)}=y_{\pi(k)}\]其中,交织地址 𝜋(𝑘) 的计算方式为:
\[\pi(k)=\left(P\left(\left\lfloor\frac{k}{R_{\text {subblock }}^{\mathrm{TC}}}\right\rfloor\right) \cdot R_{\text {subblock }}^{\mathrm{TC}}+\left(k \bmod R_{\text {subblock }}^{\mathrm{TC}}+1\right) \bmod K_\pi\right)\]- \(P(\cdot)\):列置换函数(由表决定);
- \(K_\pi=R_{\text {subblock }}^{\mathrm{TC}} \cdot C_{\text {subblock }}^{\mathrm{TC}}\):矩阵总大小(含填充位);
- 所有索引都在模 𝐾𝜋 下进行环绕操作。
相比前两个交织器:
循环右移1位,使冗余比特与前两路错位,增强统计独立性
2. 比特的收集(Bit selection)
参考标准:TS 36.211 §5.1.4.1.2
将经过子块交织后的三路比特流合并进入一个虚拟循环缓冲区(Virtual Circular Buffer),为比特选择与传输(如 HARQ 重传或速率匹配)做准备。
将长度为 𝐾𝜋 的每一路比特流依次写入缓冲区:
\[\begin{aligned} w_k & =v_k^{(0)}, & k & =0, \ldots, K_\pi-1 \\ w_{K_\pi+2 k} & =v_k^{(1)}, & k & =0, \ldots, K_\pi-1 \\ w_{K_\pi+2 k+1} & =v_k^{(2)}, & k & =0, \ldots, K_\pi-1 \end{aligned}\]- 缓冲区总长度为 3𝐾𝜋
- 校验比特采用交替方式插入
合并后的虚拟缓冲区比特顺序如下所示:
\[w=\underbrace{v_0^{(0)}, v_1^{(0)}, \ldots, v_{K_{\Pi}-1}^{(0)}}_{\text {系统位流 }}, \underbrace{v_0^{(1)}, v_0^{(2)}, v_1^{(1)}, v_1^{(2)}, \ldots, v_{K_{\Pi}-1}^{(1)}, v_{K_{\Pi}-1}^{(2)}}_{\text {校验位交替排列 }}\]3. 比特选择与修剪(Bit Selection & Pruning)
通过在虚拟循环缓冲区(Virtual Circular Buffer)中选取有效比特,跳过无效比特(NULL 填充),从而生成最终发送到物理信道的比特序列 ek
- 比特数量 𝐸 的确定:根据物理信道容量和调制方式要求动态确定
- 设置起始偏移 𝑘0:
- 起始偏移用于支持 HARQ 增量冗余机制(Incremental Redundancy)
- 使每次传输选择不同的起始位置,获得不同校验比特组合;
- 比特循环提取规则:
- 从虚拟缓冲区 {𝑤𝑘} 中,按顺序循环提取 𝐸 个有效比特;
- 跳过填充的 NULL 位(表示无效比特)
- 得到最终速率匹配输出序列:
七、码块级联
参考TS 36.211 §5.1.4.1.2以及TS 36.212 §5.3.2.5
目的:
将多个独立编码码块(Code Blocks)拼接成一个连续的传输块(Transport Block),形成最终输出到物理信道的比特流序列。
每个码块经过速率匹配模块处理,得到其对应比特输出:
\[\left\{e_0^{(r)}, e_1^{(r)}, \ldots, e_{E_r-1}^{(r)}\right\}\]其中:\(r = 0,1,2, \dots, C-1\)
按照码块编号 𝑟 从小到大(编码顺序)依次连接所有码块的比特序列,拼接形成一个完整的传输块码流:
\[\left\{f_0, f_1, \ldots, f_{E_{\text {total }}-1}\right\}\]最终生成完整的传输块比特序列,供物理层调制映射使用; 至此 LTE DLSCH 信道编码流程结束,从原始传输块输入到比特流输出全部完成。
八、LTE下行共享信道编码总结
LTE DLSCH 的信道编码流程包括:
- 对传输块添加CRC后进行码块分割与填充处理;
- 随后每个码块独立进行Turbo编码,并添加尾比特;
- 接着通过子块交织、比特收集与速率匹配生成比特流;
- 最后将多个码块的比特序列级联;
最终形成完整的编码输出,用于后续调制与物理层传输。
此过程也是通常意义所说的比特级处理,后续将进入符号级处理。
文档信息
- 本文作者:Ziyue Qi
- 本文链接:https://www.qiziyue.cn/2025/07/27/4G%E4%BF%A1%E9%81%93%E7%BC%96%E7%A0%81/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)