一、引言:5G 信道编码概述
在4G LTE中,Turbo编码作为核心信道编码方案,凭借其强大的纠错性能和实现成熟度,在多种传输场景中得到了广泛应用。
在5G中,LDPC(低密度奇偶校验码) 被引入作为数据信道的主要信道编码方式,取代了LTE中的Turbo码。
本节将系统介绍5G NR中LDPC编码流程,包括传输块CRC附加、基图选择与段划分、码字生成、速率匹配及码块级联等关键步骤。
二、5G下行信道编码流程总体介绍
5G NR 的下行共享信道(PDSCH)信道编码流程总体与4G系统类似,包括以下步骤:
传输块CRC附加:为每个传输块添加24比特的CRC,用于差错检测(见 38.212 - 7.2.1);
LDPC基图选择:根据传输块大小和调制方式选择LDPC基图(Base Graph 1 或 2),为后续编码提供结构依据(见 7.2.2);
码块分段与子块CRC附加:当传输块过大时将其分段,并对每个码块附加CRC(见 7.2.3);
信道编码:使用LDPC编码对每个码块进行独立编码,提升纠错能力(见 7.2.4);
速率匹配:通过比特选择、交织和重复/裁剪等操作使输出比特数适应物理层资源分配(见 7.2.5)。
三、传输块级 CRC 添加(Transport Block CRC Attachment)
同4G,TB级CRC附加(Transport Block CRC Attachment)用于对每个传输块(Transport Block)提供整体错误检测能力,确保数据传输的完整性。
参考 [TS 38.212 第7.2.1节 和 第5.1节]
映射顺序采用最高有效位优先(MSB),即按大端序排列。
选择规则如下:
根据传输块长度 𝐴(比特),选择CRC多项式长度:
- 长块(A > 3824): 使用24比特CRC,多项式为 CRC24A(D)
- 短块(A ≤ 3824): 使用16比特CRC,多项式为 CRC16(D)
编码过程:
- 输入比特序列:
- 在有限域 GF(2) 上,按照系统形式进行CRC编码:
- 输入序列与多项式整除,余数作为CRC附加至原始数据尾部
输出最终比特序列:
\[b_0, b_1, \ldots, b_{B-1}\]其中:
\[B = A + L\]L 位CRC长度。
总之5G中TB级CRC附加机制与LTE几乎完全一致,本质上均为在GF(2)域进行多项式除法运算。
四、LDPC基图的选择
参考TS 38.212 7.2.2
在5G NR中,LDPC信道编码使用两种基础母矩阵(Base Graph)结构,分别称为基图1和基图2。
为了在不同数据量和场景下实现性能与复杂度的权衡,5G标准根据有效载荷大小A(即传输比特长度)和编码速率R的组合来选择合适的基图:
基图的选择规则为:
\[\text { 基图 }= \begin{cases}2, & \text { 当 } A \leq 292, \text { 或 }(A \leq 3824 \text { 且 } R \leq 0.67), \text { 或 } R \leq 0.25 \\ 1, & \text { 否则 }\end{cases}\]其中:
- A:原始传输块长度;
- R:编码速率
- 基图1和基图2对应不同结构和稀疏程度的校验矩阵
性能与效率权衡:
- 基图1:适用于高码率、大数据块场景,编码效率高
- 基图2:适用于低码率、小数据块或高可靠性需求场景
五、码块分割与子块CRC附加
参考 3GPP TS 38.212 5.2.2
码块分割与子块CRC附加”阶段的主要目标是将整个传输块(Transport Block)划分为多个更小的码块(Code Block)并为每个码块分别添加CRC校验。
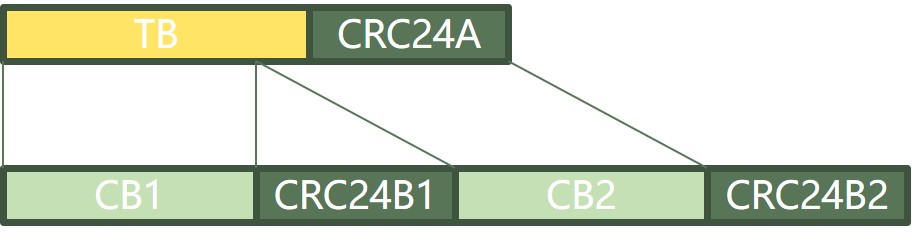
1. 输入输出
- 输入:添加过TB CRC的完整比特流
长度 B=A+24
- 输出:生成 𝐶 个码块
每个码块附加24比特子块CRC校验。
2. 最大码块长度 Kcb 的确定
LDPC编码器根据所选的基图(Base Graph)决定码块最大长度 𝐾𝑐𝑏
- 基图1:最大码块长度为 8448;
- 基图2:最大码块长度为 3840;
根据 𝐾𝑐𝑏 的大小判断是否需要码块分割。若传输块长度 𝐵>𝐾𝑐𝑏 ,则进行分割;否则直接进入编码阶段。
3. 码块数量计算
目前已知输入:
- 已添加 TB CRC 的传输块比特流,长度为 B;
- 当前选定的最大码块长度 𝐾𝑐𝑏(由所选基图决定);
📌 分两种情况处理:
case1:单码块场景(不分段)
\[B \leq K_{c b}\]- 无需拆分,设置码块数量为 𝐶=1;
- 不再添加码块级 CRC
- 输出总长度不变:𝐵′=𝐵;
case1:多码块场景(需分段)
\[B>K_{c b}\]- 需将传输块拆分成多个码块,每个码块长度最多为 𝐾𝑐𝑏−𝐿,其中 𝐿=24 是每个码块附加的 CRC 长度;
- 码块数量计算为:
- 每个码块附加 24 比特 CRC,总输出长度更新为:
该步骤确保每个码块不会超过 LDPC 编码器的最大处理能力,并为每个独立的码块单独添加 CRC 校验
4. 提升因子与码块长度计算
参考 3GPP TS 38.212 5.2.2
在 5G LDPC 编码中,为了确定最终的码块长度及编码矩阵结构,还需引入提升因子(Lifting Size)𝑍𝑐 ,用于生成 LDPC 码的实际结构。
✅ 第一步:确定基图类型对应的最小提升因子下界 𝐾𝑏
- 基图 1 固定为:
- 基图 2 根据输入长度 𝐵 动态选择:
✅ 第二步:计算每个码块的目标编码长度(不含填充)
设总输出长度为 𝐵′,码块数量为 𝐶,则每个码块需编码的目标长度为:
\[K^{\prime}=\left\lceil\frac{B^{\prime}}{C}\right\rceil\]✅ 第三步:从标准中选择合适的提升因子 𝑍𝑐
- 提升因子需满足:
- 从标准表(如 Table 5.3.2-1)中选择满足条件的最小 𝑍𝑐;
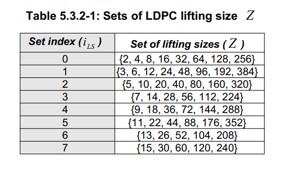
✅ 第四步:确定最终编码长度与填充位数
- 最终编码长度为:
- 基图 1:𝐾=22𝑍𝑐
- 基图 2:𝐾=10𝑍𝑐
- 若实际比特数小于编码矩阵大小,则需填充:
5. 码块分割及码块级CRC添加
- 将大传输块拆分为多个适合编码的码块;
- 为每个码块添加 CRC 校验位,提供单独的错误检测能力;
- 填充空白比特位(Filler Bits),确保码块长度与 LDPC 校验矩阵匹配。
(a) 前置条件
- 传输块 TB 已经添加了 TB 级 CRC;
- TB 被分割为 𝐶 个码块;
- 每个码块后续将分别输入 LDPC 编码器。
| 操作 | 内容说明 |
|---|---|
| 数据分配 | 将 CRC 后的比特流均匀划分为 C 个码块 |
| 码块级 CRC 添加 | 若 C > 1,则为每个码块添加 24 位 CRC |
| 长度对齐 | 对不足 LDPC 编码长度的码块添加填充位(Filler Bits),通常填“0”且不发送 |
(b) 关键参数梳理
- 输入比特流:原始比特流:
其中 \(B'=B+C\cdot L\),为添加子块CRC与填充后的总长度;
- 码块数量:𝐶
- 码块长度(不含填充):𝐾′
- CRC长度:24
(c) 具体步骤说明
初始化:设置比特计数指针 𝑠=0,用于在原始比特流中按顺序输入数据。
循环写入比特流到各码块:
添加CRC校验位(当 𝐶>1 时)
填充空位(Filler Bits):对于 𝑘=𝐾′ 到 𝐾−1,将比特填充为 NULL。
✅ 最终输出
- 𝐶 个码块,每个码块长度均为 𝐾,包含原始数据、CRC及填充位;
- 输出比特流供下一步 LDPC 编码使用:
(d) 示例验证
以下代码完整地实现了 5G NR 下 LDPC 信道编码流程中的码块分割与子块 CRC 添加,并与 MATLAB 内置函数进行了对比:
传输块生成与传输块级 CRC 添加
A = 34407; % 原始传输块大小
trBlk = randi([0 1],A,1); % 生成随机传输块数据
R = 1/3; % 编码率设置
% 选择 CRC 类型(16位或24位)
if A > 3824
L = 24; TB_CRC_type = '24A';
else
L = 16; TB_CRC_type = '16';
end
crced = nrCRCEncode(trBlk, TB_CRC_type); % 添加 CRC
基图选择(Base Graph Selection)
if A <= 292 || (A <= 3824 && R <= 0.67) || R <= 0.25
bgn = 2;
else
bgn = 1;
end
码块分割与子块 CRC 添加(自定义函数)
c_blocks = codeBlockSegmentationAndCRC(crced, bgn);
以下函数完成:
- 判断是否需要分块;
- 计算码块数量 C;
- 子块 CRC(CRC24B)添加(当 C > 1);
- 根据基图确定 Kb 与 Zc,最终确定 K;
- 将原始数据填入每个码块中;
- 用 -1 填充空位,标记 NULL。
function c_blocks = codeBlockSegmentationAndCRC(b, baseGraph)
% 5G LDPC: 码块分割及子块CRC添加
% 输入:
% b : 原始传输块比特流(0/1数组)
% baseGraph : LDPC基图编号(1或2)
% 输出:
% c_blocks : C×K 矩阵,每行为一个码块(包含数据、CRC和填充)
% ----------------- 参数设置 -----------------
L_crc = 24; % CRC24B 长度
B = length(b); % 原始比特数
% 最大码块长度 K_cb
if baseGraph == 1
K_cb = 8448;
elseif baseGraph == 2
K_cb = 3840;
else
error('Invalid baseGraph. Use 1 or 2.');
end
% ----------------- 判断是否需要分块 -----------------
if B <= K_cb
C = 1;
L = 0;
else
C = ceil(B / (K_cb - L_crc));
L = L_crc;
end
% 总比特长度(包含子块CRC)
B_prime = B + C * L;
% 码块长度(不含填充)
K_prime = ceil(B_prime / C);
if baseGraph == 1
Kb = 22;
else
if B > 640
Kb = 10;
elseif B > 560
Kb = 9;
elseif B > 192
Kb = 8;
else
Kb = 6;
end
end
Zlist = [2:16 18:2:32 36:4:64 72:8:128 144:16:256 288:32:384];
Zc = min(Zlist(Kb*Zlist >= K_prime));
if baseGraph == 1
K = 22*Zc;
else
K = 10*Zc;
end
% ----------------- 数据写入各码块 -----------------
c_blocks = nan(K, C); % 用NaN标记填充值
s = 1;
for r = 1:C
for k = 1:(K_prime - L)
if s <= length(b)
c_blocks(k, r) = b(s);
s = s + 1;
else
c_blocks(k, r) = 0; % 不足补0
end
end
% ----------------- 添加CRC(当 C > 1) -----------------
if C > 1
msg = c_blocks(1:(K_prime - L), r);
msg_crc = nrCRCEncode(msg,"24B");
c_blocks(1:K_prime, r) = msg_crc;
end
% ----------------- 填充位 NULL -----------------
if K_prime < K
c_blocks((K_prime + 1):K, r) = -1; % 标记为 NULL
end
end
end
六、5G LDPC 编码
1. 输入输出
在完成前一阶段的码块分割及码块级CRC添加之后:
- 原始传输块被分割为 𝐶 个码块(Code Block)
- 每个码块的输入比特流记为:
其中 𝑟 为码块索引(第 𝑟 个码块),Kr 为第 r 个码块的比特数
输入维度:
| 基图编号 | 输入长度 \(K\) |
|---|---|
| BG1 | \(K = 22 \cdot Z_c\) |
| BG2 | \(K = 10 \cdot Z_c\) |
- 每个码块单独进行 LDPC 编码(依照 3GPP TS 38.212 §5.3.2 进行)
- 每个码块的编码输出为:
即第 𝑟 个码块的编码比特序列,长度为 𝑁𝑟。
编码输出比特长度由 基图类型 和 提升值 𝑍𝑐共同决定:
| 基图编号 | 码字长度 \(N\) |
|---|---|
| 基图 1 | \(N = 66 Z_c\) |
| 基图 2 | \(N = 50 Z_c\) |
2. 编码前数据准备
依据 TS 38.212 第 5.3.2 节
编码器的输入为维度为 [𝐾,𝐶] 的比特矩阵,其中每列为一个码块。由于之前的码块填充处理可能存在“无效比特”(-1 填充值),标准规定:
在 LDPC 编码前,填充值必须被替换为全 0。
替换逻辑:
- 如果比特为
,则在编码输入中置为 0; - 否则保留原始有效值。
即:
\[c_k= \begin{cases}0, & \text { if } c_k=<\mathrm{NULL}> \\ c_k, & \text { otherwise }\end{cases}\]至此,送入 LDPC 编码器的所有信息比特准备完成,每列为一个独立码块的编码输入,即将进入 LDPC 编码阶段。
3. LDPC 编码
TS 38.212 5.3.2
(a) 编码输入结构
编码器的输入比特流为每个码块比特:
\[\mathbf{c}=\left[c_0, c_1, \ldots, c_{K-1}\right]^T\]K:取决于基图(BG1 为 22𝑍𝑐,BG2 为 10𝑍𝑐)
LDPC 编码器的任务是基于输入 𝑐 生成校验比特 𝑤,使得整个码字满足奇偶校验关系:
\[\mathbf{x}=\left[\begin{array}{l} \mathbf{c} \\ \mathbf{w} \end{array}\right] \quad \text { 使得 } \quad H \cdot \mathbf{x}=\mathbf{0}\]其中:
- 𝐻:为 LDPC 的校验矩阵(取决于基图)
- 𝑤
- w:为 𝑁−𝐾 个校验比特,维度 (𝑁−𝐾)×1
- N:LDPC 编码块长度(BG1 为 66𝑍𝑐,BG2 为 50𝑍𝑐)
LDPC 编码是一个线性方程求解问题,在有限域 GF(2) 中进行。
(b) 基图矩阵的构造与获取
🧩 什么是基图矩阵 \(H_{BG}\)
LDPC 编码器的核心依赖一个稀疏的校验矩阵 𝐻。此矩阵不是直接使用完整矩阵表示,而是通过 基图矩阵(Base Graph) 与 提升因子 𝑍𝑐 组合生成。
两个维度:
| 类型 | 矩阵维度 |
|---|---|
| 基图 1 | \(46 \times 68\) |
| 基图 2 | \(42 \times 52\) |
基图元素由标准表格定义,参见 3GPP TS 38.212 中:
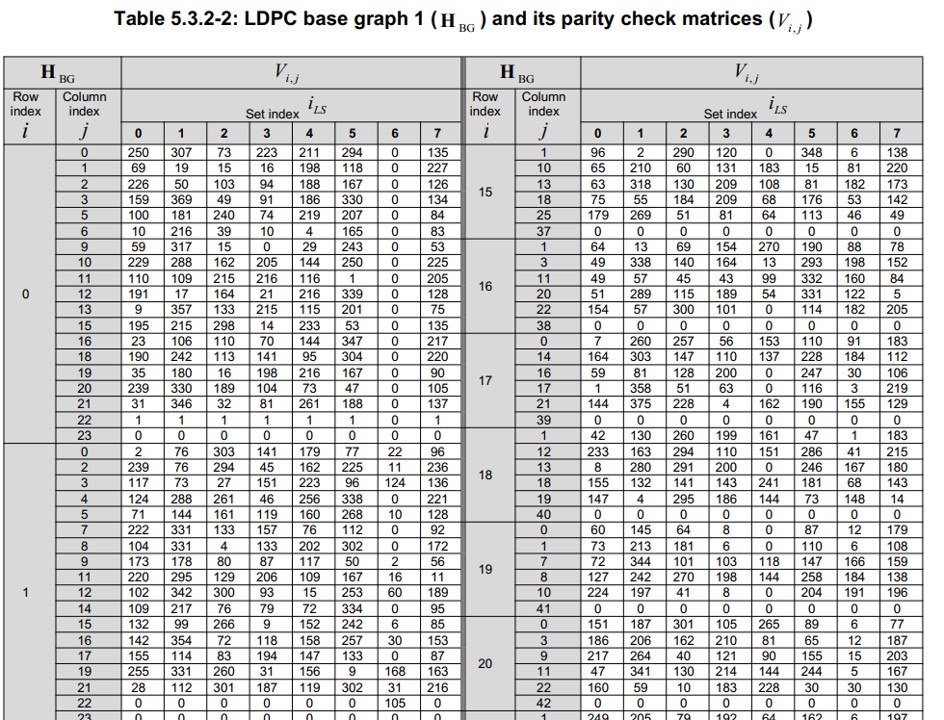
- 表 5.3.2-2:BG1
- 表 5.3.2-3:BG2
元素含义如下:
- 若 \(V_{i, j}=v\),表示在位置 (𝑖,𝑗) 处放置一个 向右移位 𝑣 的单位循环矩阵 \(I_v\)
- 若为空值,表示该位置没有值(即为零矩阵)
(c) 实际编码矩阵 𝐻 生成规则
通过提升因子扩展基图矩阵,得到 LDPC 编码器使用的实际稀疏校验矩阵 𝐻,其维度满足编码所需。
完整的 LDPC 校验矩阵通过如下方式构建:
\[H=\left[V_{i, j}\right]_{m \times n} \otimes I_{Z_c}\]其中:
- m,n 是基图维度(例如 BG1 为 46×68)
- \(I_{Z_c}\) 为 𝑍𝑐×𝑍𝑐的单位循环移位矩阵
从另一个角度看,构造规则如下:
每个基图矩阵元素 𝑉𝑖,𝑗 被替换为一个 𝑍𝑐×𝑍𝑐 的子矩阵:
| \(V_{i,j}\) 类型 | 替换矩阵类型 | 含义 |
|---|---|---|
| 空值 | 全零矩阵 | 用 \(Z_c \times Z_c\) 的全 0 矩阵替代 |
| 0 | 单位矩阵 | 替换为 \(Z_c \times Z_c\) 单位矩阵 |
| $v>0$ | 循环置换矩阵 | 替换为单位矩阵右移 \(v\) 位得到的循环置换矩阵 \(P_{i,j}\) |
循环置换矩阵定义为将单位矩阵 I 循环右移 Pi,j 次:
\[P_{i, j}=\bmod \left(V_{i, j}, Z_c\right)\]例如对于一个三维矩阵,若 \(P_{i, j}=2\),则循环置换矩阵为:
\[\left[\begin{array}{lll} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right]\]即将单位矩阵每一行循环右移 2 位。
扩展后编码矩阵H维度:
| 基图类型 | 基图维度 | 扩展后编码矩阵维度(乘 \(Z_c\)) |
|---|---|---|
| BG1 | \(46 \times 68\) | \(46Z_c \times 68Z_c\) |
| BG2 | \(42 \times 52\) | \(42Z_c \times 52Z_c\) |
(d) 送入编码器前关键参数总结
| 参数名称 | 含义 | 计算方式 |
|---|---|---|
| 奇偶校验矩阵 \(\mathbf{H}\) | 编码使用的稀疏矩阵,维度为 \(m \times n\) | 通过基图矩阵 \(H_{BG}\) 扩展得到,依赖提升因子 \(Z_c\) |
| 码字总长度 \(n\) | 编码输出比特数 | \(n = \text{BlockLength} = N = \text{列数} \times Z_c\) BG1: \(68 \times Z_c\) BG2: \(52 \times Z_c\) |
| 校验位数 \(m\) | 奇偶校验比特数量 | \(m = \text{NumParityCheckBits} = \text{行数} \times Z_c\) BG1: \(46 \times Z_c\) BG2: \(42 \times Z_c\) |
| 信息位数 \(k\) | 原始输入比特数(含 CRC、填充) | \(k = n - m\) BG1: \(22 \times Z_c\) BG2: \(10 \times Z_c\) |
| 编码码率 \(R\) | 有效信息与编码输出的比值 | \(R = \frac{k}{n}\) |
示例计算:
假设:
- 提升因子 𝑍𝑐=192
- 基图选择:BG1(BaseGraph 1)
| 参数项 | 数值 |
|---|---|
| 校验矩阵维度 | \(46 \times 68\) × 192 = 8832 × 13056 |
| 校验位数 \(m\) | \(46 \times 192 = 8832\) |
| 总码长 \(n\) | \(68 \times 192 = 13056\) |
| 信息位数 \(k\) | \(22 \times 192 = 4224\) |
| 编码码率 \(R\) | \(\frac{4224}{13056} \approx 0.3235\) |
(e) 编码矩阵结构解析与编码方程建立
在 LDPC 编码中,需满足如下同余条件(GF(2)域):
\[\mathbf{H} \cdot\left[\begin{array}{c} \mathbf{c} \\ \mathbf{w} \end{array}\right]=0\]其中:
- c:待编码的信息比特;
- w:要生成的校验比特;
- H:编码矩阵(由基图 H_BG 扩展生成的稀疏大矩阵)
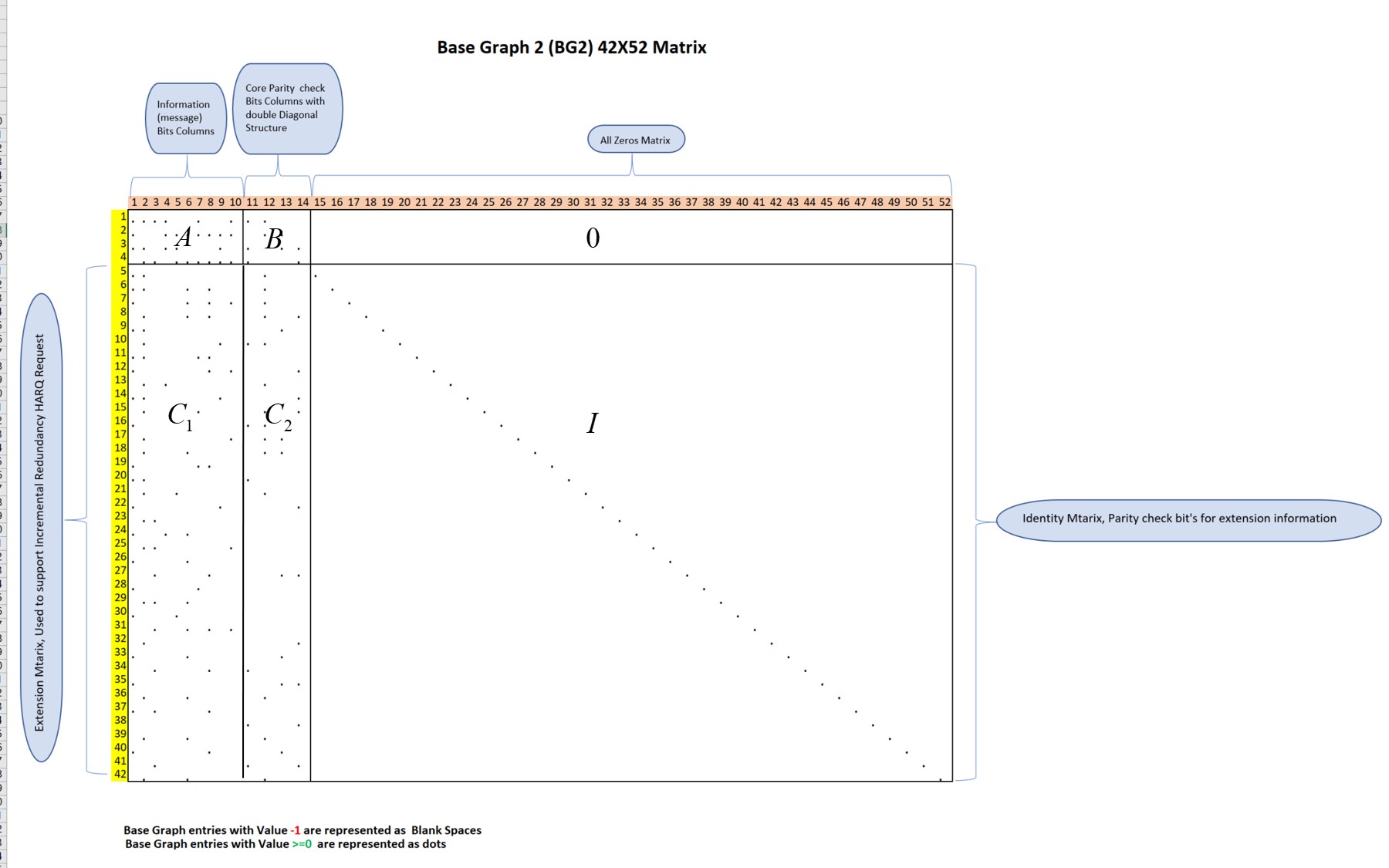
解稀疏矩阵H和解基图矩阵类似,此处为了方便说明此处以HBG代替H,省略Zc,其中每个元素都是一个 ZcxZc 维度矩阵。
H_BG 矩阵被划分为如下 6 个子矩阵:
\[H_{B G}=\left[\begin{array}{cc|cc} A & B & \mathbf{0} & \mathbf{0} \\ C_1 & C_2 & P_b^T & I \end{array}\right]\]编码的目标是通过求解:
\[P_b \quad P_c\]使整体满足方程:
\[H_{B G}\left[\begin{array}{l} S^T \\ P_b^T \\ P_c^T \end{array}\right]=0\]即:
\[\left[\begin{array}{ccc} A & B & 0 \\ C_1 & C_2 & I \end{array}\right]\left[\begin{array}{l} S^T \\ P_b^T \\ P_c^T \end{array}\right]=0\]即:
\[\begin{aligned} & A S^T+B P_b^T=0^T \\ & C_1 S^T+C_2 P_b^T+P_c^T=0 \end{aligned}\]其中:
\[A=\left[\begin{array}{cccc} a_{1,1} & a_{1,2} & \ldots & a_{1, K} \\ a_{2,1} & a_{2,2} & \ldots & a_{2, K} \\ a_{3,1} & a_{3,2} & \ldots & a_{3, K} \\ a_{4,1} & a_{4,2} & \ldots & a_{4, K} \end{array}\right]\] \[C_1=\left[\begin{array}{cccc} c_{1,1} & c_{1,2} & \ldots & c_{1, K} \\ c_{2,1} & c_{2,2} & \ldots & c_{2, K} \\ \vdots & \vdots & \ddots & \\ c_{M-4,1} & c_{M-4,2} & \ldots & c_{M-4, K} \end{array}\right]\] \[C_2=\left[\begin{array}{cccc} c_{1, K+1} & c_{1, K+2} & c_{1, K+3} & c_{1, K+4} \\ c_{2, K+1} & c_{2, K+2} & c_{2, K+3} & c_{2, K+4} \\ \vdots & \vdots & \ddots & \\ c_{M-4, K+1} & c_{M-4, K+2} & c_{M-4, K+3} & c_{M-4, K+4} \end{array}\right]\]对于子矩阵 B,总结只有四种情况(BG1有两种,BG2有两种),此处给出BG2的情况:
\[H_{B G 2_{-} B 1}=\left[\begin{array}{cccc} 0 & 0 & -1 & -1 \\ -1 & 0 & 0 & -1 \\ 1 & -1 & 0 & 0 \\ 0 & -1 & -1 & 0 \end{array}\right]\] \[H_{B G 2_{-} B 2}=\left[\begin{array}{cccc} 1 & 0 & -1 & -1 \\ -1 & 0 & 0 & -1 \\ 0 & -1 & 0 & 0 \\ 1 & -1 & -1 & 0 \end{array}\right]\]现在重新整理:
目的是求解:
\[\begin{aligned} & A S^T+B P_b^T=0^T \\ & C_1 S^T+C_2 P_b^T+P_c^T=0 \end{aligned}\]- 首先求解:
- 已知A;
当:
\[B=H_{B G 2 \_B 1}=\left[\begin{array}{cccc} 0 & 0 & -1 & -1 \\ -1 & 0 & 0 & -1 \\ 1 & -1 & 0 & 0 \\ 0 & -1 & -1 & 0 \end{array}\right]\]- 0表示取原矩阵
- 1表示对单位阵循环右移
- -1表示取 0 矩阵
转换为求解如下方程:
\[\left\{\begin{array}{l} \sum_{j=1}^K a_{1, j} s_j+p_{b_1}+p_{b_2}=0 \\ \sum_{j=1}^K a_{2, j} s_j+p_{b_2}+p_{b_3}=0 \\ \sum_{j=1}^K a_{3, j} s_j+p_{b_1}^{(1)}+p_{b_3}+p_{b_4}=0 \\ \sum_{j=1}^K a_{4, j} s_j+p_{b_1}+p_{b_4}=0 \end{array}\right.\]此处不妨令:
\[\lambda_i=\sum_{j=1}^K a_{i, j} s_j \quad i=1,2,3,4\]所有矩阵都遵循异或加法,四式相加后易得:
\[\left\{\begin{array}{l} p_{b_1}^{(1)}=\sum_{i=1}^4 \lambda_i \\ p_{b_2}=\lambda_1+p_{b_1} \\ p_{b_3}=\lambda_2+p_{b_2} \\ p_{b_4}=\lambda_4+p_{b_1} \end{array}\right.\]其它BG情况和B的情况同理。
求解出Pb后,可根据下公式求解Pc:
\[C_1 S^T+C_2 P_b^T+P_c^T=0\]即:
\[P_{c i}=\sum_{j=1}^K c_{i, j} s_j+\sum_{j=1}^4 c_{i,(K+j)} p_{b j}\]总结整个编码过程:
本质是求解:
\[\left[\begin{array}{ccc} A & B & 0 \\ C_1 & C_2 & I \end{array}\right]\left[\begin{array}{l} S^T \\ P_b^T \\ P_c^T \end{array}\right]=0\]以 BG2 的\(B=\left[\begin{array}{cccc} 0 & 0 & -1 & -1 \\ -1 & 0 & 0 & -1 \\ 1 & -1 & 0 & 0 \\ 0 & -1 & -1 & 0 \end{array}\right]\)为例:
可以求出校验位:
\[\left\{\begin{array}{l} p_{b_1}^{(1)}=\sum_{i=1}^4 \lambda_i \\ p_{b_2}=\lambda_1+p_{b_1} \\ p_{b_3}=\lambda_2+p_{b_2} \\ p_{b_4}=\lambda_4+p_{b_1} \end{array} \quad P_{c i}=\sum_{j=1}^K c_{i, j} s_j+\sum_{j=1}^4 c_{i,(K+j)} p_{b j}\right.\]其中 \(\lambda_i=\sum_{j=1}^K a_{i, j} s_j \quad i=1,2,3,4\)
由此编码过程完成。即协议中的w求出。
4. 编码输出构成与截取
TS 38.212 §5.3.2.2
将编码器输出的 奇偶校验位 𝑤 与原始信息比特序列 𝑐 组合,生成最终的编码输出比特序列 𝑑
- 跳过前 2Zc 位信息比特并拼接奇偶校验位
信息比特:
\[\mathbf{c}=\left[c_0, c_1, \ldots, c_{K-1}\right]\]奇偶校验比特:
\[\mathbf{w}=\left[w_0, w_1, \ldots, w_{N-K-1}\right]\]拼接在 𝑐 后得到最终输出序列:
\[d=[\underbrace{c_{2 Z_c}, c_{2 Z_c+1}, \ldots, c_{K-1}}_{\text {原始数据, 跳 过前 } 2 Z_c \text { 位 }}, \underbrace{w_0, w_1, \ldots, w_{N+2 Z-K-1}}_{\text {校验位 }}]\]- 填充值(Filler Bits)还原
✅ 在构成最终编码输出比特序列 d 时,原来信息比特中是 NULL(-1)的地方,需要将这些位置还原为 NULL(编码时置为0)
经过此步骤,最终完成 LDPC 编码器中 “数据输出”构成的封装流程。
5. LDPC编码小结
下图给出LDPC编码模块的数据维度变化情况:

下图以BG1为例,给出一个码块数据编码全过程:

七、速率匹配
3GPP TS 38.212 第 7.2.5 节
速率匹配主要由以下两个过程构成:
- 比特选择(Bit Selection)
- 比特交织(Bit Interleaving)
其作用:
根据无线信道资源调整编码后的比特长度,使其精确匹配调制器所需的比特数量。
1. 输入输出:
- 输入:
编码后的码块比特序列:
\[d_{r, 0}, d_{r, 1}, \ldots, d_{r, N_r-1}\]其中 𝑟 为第 𝑟 个码块,𝑁𝑟 为该码块的编码输出比特数。
- 输出:
速率匹配后的比特序列:
\[f_{r, 0}, f_{r, 1}, \ldots, f_{r, E_r-1}\]其中 𝐸𝑟 是速率匹配输出的目标比特数
2. 比特选择(Bit Selection)
核心功能:从 LDPC 编码输出中选出恰好 𝐸𝑟 个比特,用于后续调制映射,匹配无线物理资源配置。
- 循环缓冲区(Circular Buffer):
- LDPC 编码输出将被顺序写入一个长度为 𝑁𝑐𝑏 的循环缓冲区。
- 对 DLSCH 场景来说,𝑁𝑐𝑏=𝑁,即完整的码字长度。
- 缓冲区会按 冗余版本 RV 不同,从不同位置开始读取,具体参见协议表5.4.2.1-2。
- 比特选择过程中需跳过所有 NULL(即原始填充位)比特。
- 目标输出比特数
- 指每个码块速率匹配后需要提取的比特数量
- 计算方式与调制方式、传输层参数等相关
3. 比特交织(Bit Selection)
通过打乱比特顺序,避免连续比特受同一突发干扰破坏;
有效提升纠错性能。
输入输出:
输入:比特选择输出序列
\[e_0, e_1, \ldots, e_{E_r-1}\]输出:交织后比特序列
\[f_0, f_1, \ldots, f_{E_r-1}\]交织操作(横进竖出):
- 将输入序列以行优先方式填入\(\frac{E_r}{Q_m} \times Q_m\)维度的矩阵中
- 按列优先顺序输出比特。
4. 速率匹配小结
- 比特选择确保从编码结果中抽取所需比特数,跳过填充值,并可通过起始位置实现RV的多版本支持;
- 比特交织则为进一步增强传输可靠性提供支持
二者共同完成了对原始LDPC编码比特的处理,为调制映射做好了准备。
八、码块级联
- 将前面经过 LDPC 编码 → 速率匹配 的多个码块(Code Blocks)合并
- 拼接形成一个完整的传输块(Transport Block)
- 输出最终送往物理层调制的完整比特序列
拼接过程:
输入:
- 来自速率匹配模块的各码块比特序列:
输出:
传输块总比特序列:
\[g_0, g_1, \ldots, g_{G-1}\]其中:
\[G=\sum_{r=0}^{C-1} E_r\]即为所有码块速率匹配后的比特数之和。
📋 规则:
- 不涉及任何复杂变换,仅将各码块的比特按照顺序拼接输出;
至此整个 5G NR 的 DLSCH 信道编码过程完成
九、LDPC 编码过程总结
5G NR 的 DLSCH 信道编码过程包括多个有序步骤,依次对原始数据进行传输块级 CRC 添加、码块分割与子块 CRC 添加、填充处理与 LDPC 编码、速率匹配以及码块级联。
逐步将原始数据转化为适配物理信道传输的编码比特流,是实现 5G 高速可靠通信的核心流程。
文档信息
- 本文作者:Ziyue Qi
- 本文链接:https://www.qiziyue.cn/2025/07/28/5G%E4%BF%A1%E9%81%93%E7%BC%96%E7%A0%81/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)