一、判决反馈均衡 DFE 与基本工作流

DFE（Decision-Feedback Equalizer，判决反馈均衡器）是一种非线性均衡器，用来在频率选择性信道里消除符号间干扰（ISI）。

它由两条滤波支路组成：

前向滤波器（FF/Feedforward）处理接收端输入样本；

反馈滤波器（FB/Feedback）利用已经判决出的历史符号来抵消由它们引起的后游 ISI（post-cursor ISI）。

设发送符号 $a[i]$, 离散信号冲激响应为 $h[i]$，接收噪声为 $v[n]$，则等效接收序列为

DFE的输出由两部分相见得到：

其中：

• $\mathbf{u}[n]$：当前时刻前向延迟线中的接收样本向量；
• $ \hat{\mathbf{d}}[n-1] = [\hat{\mathbf{a}}[n-1], \hat{\mathbf{a}}[n-2],…]$：已判决过的历史符号；
• $\mathbf{w}$、$\mathbf{b}$：前向/反馈权值

二、SC-FDE：线性均衡 vs IBDFE（块迭代频域判决反馈）

BENVENUTO N， TOMASIN S． Iterative design and detection of a DFE in the frequency domain［J］．IEEE Trans． Communications， 2005， 53( 11) :1867－1875

1. 系统模型

目标：在单载波频域均衡（SC-FDE）框架下：

• 实现线性均衡（MMSE / 可选 ZF），
• 复刻频域块迭代判决反馈均衡器（IBDFE），

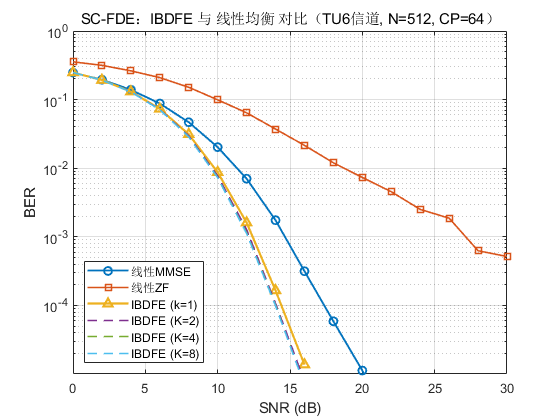
对比其在多径块衰落信道（EVA/TU6）上的 BER–SNR 性能。

发端与收端：

• 发端：比特 → QPSK → 长度 NFFT 的时域块 s_time → 加 CP（长度 CP）→ 发送。

• 信道：多径 h_time，接收 r_time = h * x + w；噪声功率设置为

  \[\sigma^2 = \frac{1}{\text{SNR}_{\text{lin}}}\]
• 收端：去 CP → 取 NFFT 点 → FFT 得到 R_f；信道频响 H_f = FFT{h_time, NFFT}。

2. 线性均衡算法

ZF：

Wzf = 1./(Hf + eps)

线性 MMSE：

其中 N0 ≈ sigma2

代码：

N0 = sigma2;
Wmmse = conj(Hf)./(abs(Hf).^2 + N0)；

3. IBDFE 基本思想

(a) 判决反馈的频域块结构

IBDFE 在频域同时设计前向滤波 $C^{(l)}(k)$ 与反馈滤波 $B^{(l)}(k)$（第 $l$ 轮迭代）：

U_f   = C .* R + B .* Shat_prev;

IFFT 得到 $u^{(l)}(n)$，判决得到符号 $\hat d^{(l)}(n)$，再 FFT 为 $\widehat{S}^{(l)}(k)$，进入下一轮。

核心是构造 $C^{(l)},B^{(l)}$ 使残余ISI与噪声最小、且不放大误差扩散。文献里用均值近似把逐频功率项集中为标量，易实现。

(b) 相关因子 $\rho$

$\rho$ 描述“当前判决”与“真实符号”的相关度，越接近 1，表示判决越可信；越小表示判决不可靠。 用 “MMSE-like 噪声感知” 估计：

此处对所有 $k$ 取均值。

num = (R .* conj(H)) ./ (abs(H).^2 + sigma2) .* conj(Shat);
rho_est = (1-eta1) * mean(num);

(c) 均值近似下的 C/B/γ/Φ

文献采用均值近似写法：

• 令发送块平均频域功率 $M_S=\mathbb{E}

  S(k)

  ^2$

MSp = mean(abs(Sp).^2);

• 判决功率 $M_{\hat S}=\mathbb{E}

  \widehat S(k)

  ^2$；

MS_shat = mean(abs(Shat_prev).^2);

• 噪声“块能量”近似 $M_w = NFFT\cdot \sigma^2$。

Mw = NFFT * sigma2;

相关公式：

denom = Mw + (MSp - (abs(rho)^2) / MS_shat ) .* (abs(H).^2);
Phi   = mean( (abs(H).^2) ./ denom );

gamma = (MSp * Phi) / (1 + (abs(rho)^2 / MS_shat * Phi));

numC  = conj(H) * MSp * ( 1 - (abs(rho)^2) / (MS_shat*MSp) * gamma );
denC  = Mw + MSp * ( 1 - (abs(rho)^2) / (MS_shat*MSp) ) .* (abs(H).^2);
 C   = numC ./ (denC + 1e-18);

B     = - rho / MS_shat .* ( H .* C - gamma );

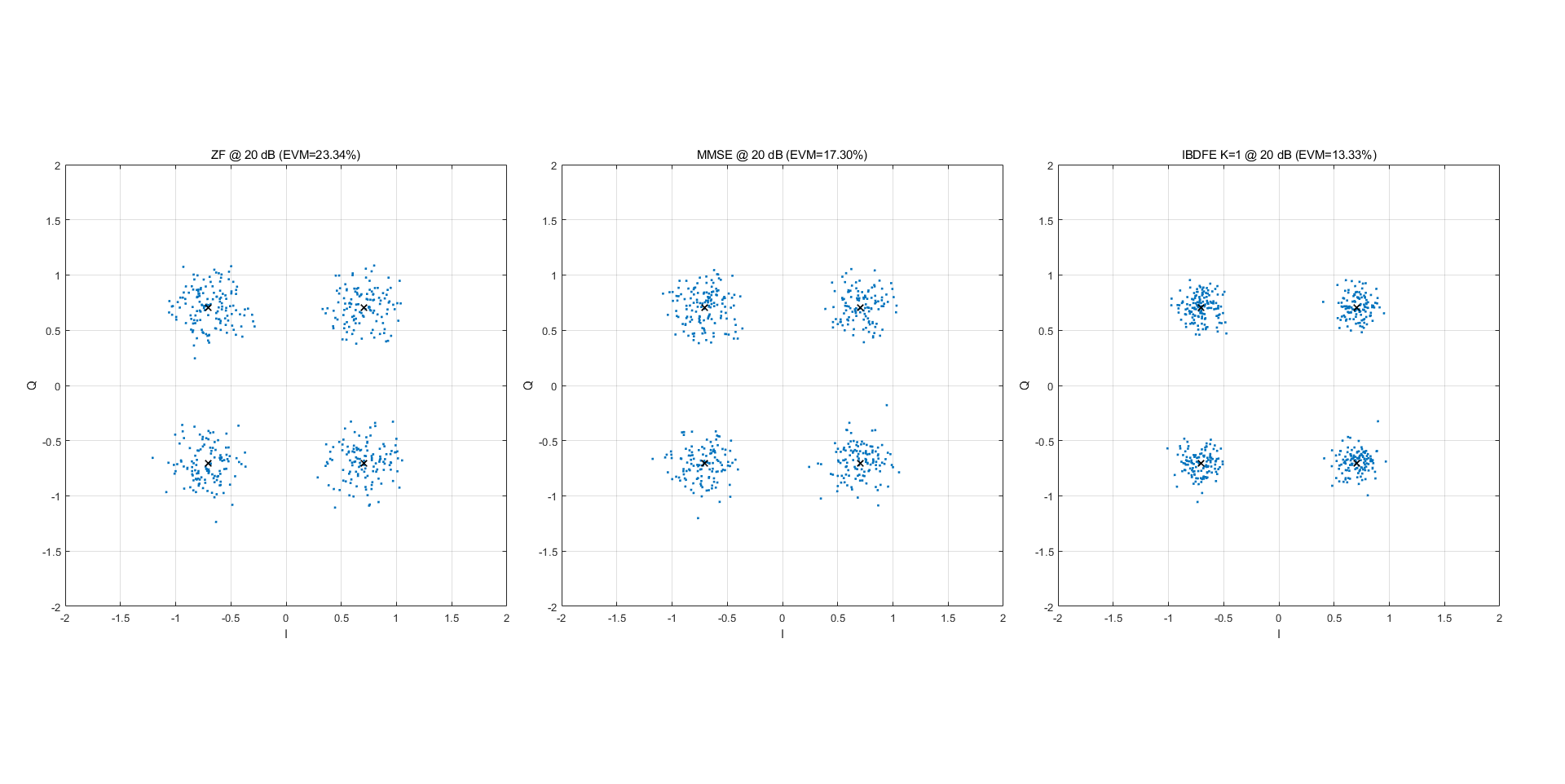
4. 仿真复刻结果

EVA 信道：

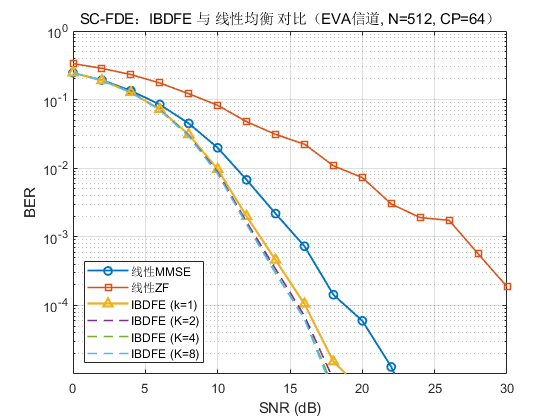
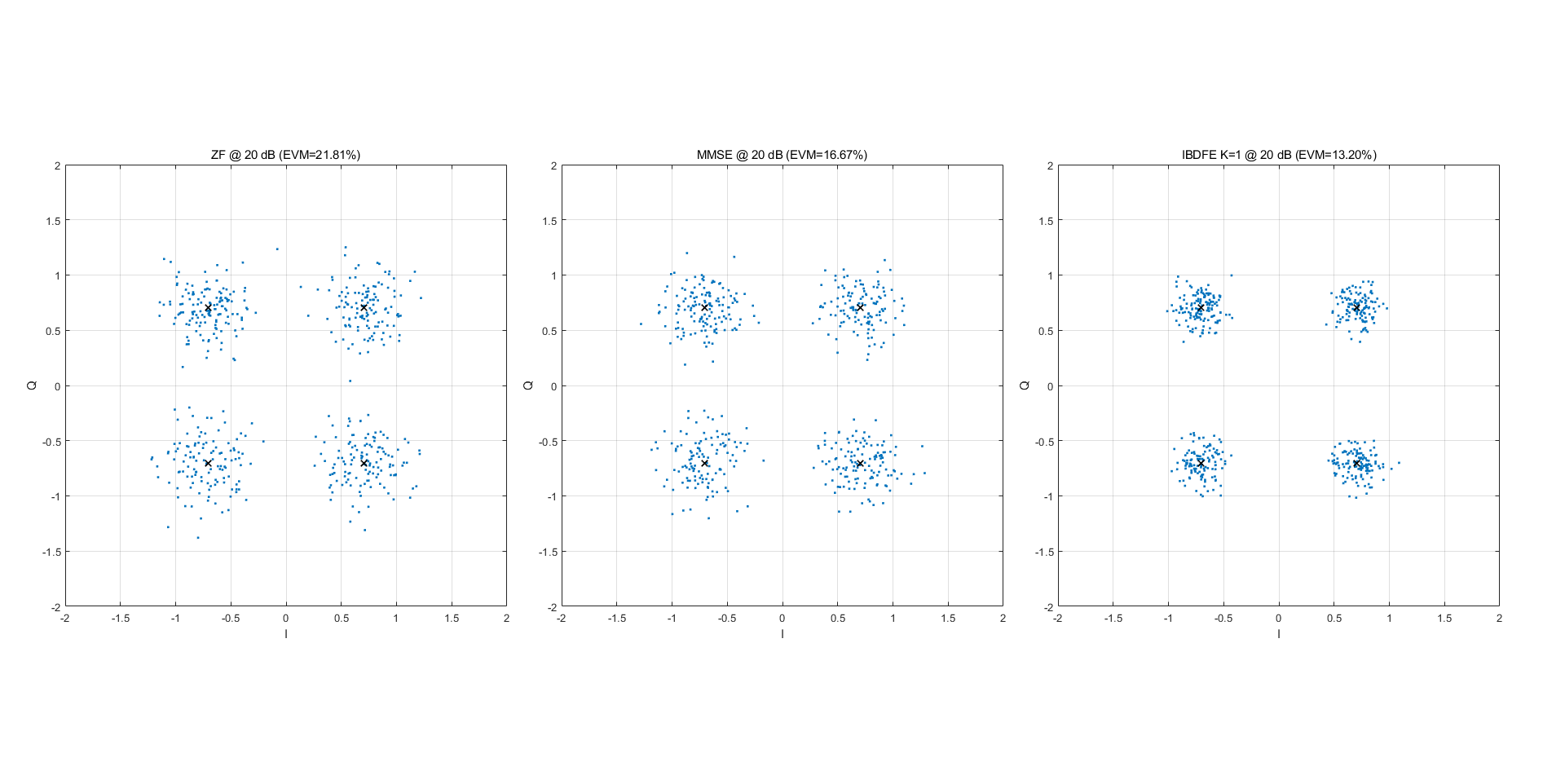
TU6 信道：