单载波判决反馈均衡
前文链接已经介绍了块迭代的单载波判决反馈均衡的原理。
其中前馈滤波器框图如下:
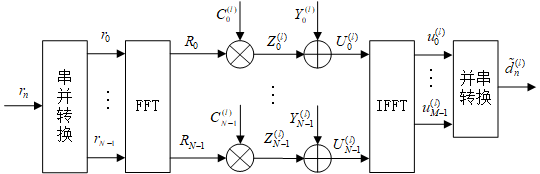
反馈滤波器框图如下:
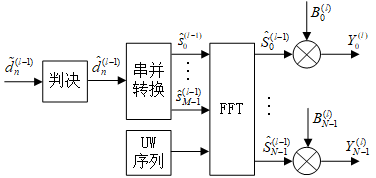
其前馈滤波器系数为:
\[C_k^{(l)}=\frac{H_k^*}{M_W+M_{S_k}\left(1-\frac{\left|r_{S_k, \hat{S}_k^{(l-1)}}\right|^2}{M_{\hat{S}_k^{(l-1)}} M_{S_k}}\right)\left|H_k\right|^2}, k=0,1, . ., N-1\]反馈滤波器系数为:
\[B_k^{(l)}=-\frac{r_{S_k, \hat{S}_k^{(l-1)}}}{M_{\hat{S}_k^{(l-1)}}}\left[H_k C_k^{(l)}-\gamma^{(l)}\right]\]其中:
\[\gamma^{(l)}=\sum_{k=0}^{N-1} H_k C_k^{(l)}\]低复杂度块迭代判决反馈均衡
块迭代的判决反馈均衡算法需要计算相关因子,复杂度非常高。
文献提出在低信噪比下,通过统计每次迭代判决输出的误码率取消相关因子的计算,每次迭代反馈均衡器系数不更新。
设第\(l-1\)次迭代发送信号\(S_k\)与判决检测信号\(\hat{S}_k^{(l-1)}\)关系:
\[\hat{S}_k^{(l-1)}=S_k+\Psi_k^{(l-1)}, \quad 0 \leq k \leq N-1\]带入公式:
\[\boldsymbol{U}^{(l)}=\boldsymbol{Z}^{(l)}+\boldsymbol{Y}^{(l)}\]得到:
\[U_k^{(l)}=C_k^{(l)} R_k+B_k\left(S_k+\Psi_k^{(l-1)}\right), \quad k=0,1, \cdots, N-1\]前文链接定义的代价函数为:
\[\begin{aligned} J_{\mathrm{HD}}^{(l)} & =\frac{1}{N^2} \sum_{k=0}^{N-1} E\left[\left|\left(C_k^{(l)} H_k-1\right) S_k+C_k^{(l)} W_k+B_k^{(l)} \hat{S}_k^{(l-1)}\right|^2\right] \end{aligned}\]带入 \(\hat{S}_k^{(l-1)}\):
\[\begin{aligned} J_{\mathrm{HD}}^{(l)} & =\frac{1}{N^2} \sum_{k=0}^{N-1} E\left[\left|\left(C_k^{(l)} H_k-1\right) S_k+C_k^{(l)} W_k+B_k^{(l)}\left(S_k+\Psi_k^{l-1}\right)\right|^2\right] \\ & =\frac{1}{N^2} \sum_{k=0}^{N-1}\left\{\left|C_k^{(l)}\right|^2 M_W+\left|C_k^{(l)} H_k-1\right|^2 M_{S_k}+\left|B_k^{(l)}\right|^2 \sigma_{\Psi^{(l-1)}}^2\right. \\ & \left.+2 \Re\left[B_k^{(l)^*}\left(C_k^{(l)} H_k+B_k^{(l)}-1\right) \Gamma^{(l-1)}\right]\right\} \end{aligned}\]文档信息
- 本文作者:Ziyue Qi
- 本文链接:https://www.qiziyue.cn/2025/07/10/%E7%AE%80%E5%8C%96%E5%88%A4%E5%86%B3%E5%8F%8D%E9%A6%88%E5%9D%87%E8%A1%A1/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)